triangles
circles
surprise
other shapes
angles
100
prove that tanx=sinx/cosx
(o/h)(h/a)
the Hs cancel out...
o/a=tanx
100
what is pi?
the ratio of the circumference of a circle to its diameter
100
At a certain time of day, a 25-foot telephone pole casts a 10-foot shadow. At that same time, how high would a tree have to be in order to cast a 25-food shadow?
62.5 feet. Proportional reasoning with similar triangles.
100
what is the perimeter of a square that has area 25?
20
100
what are the angle measurements?
50° and 50°
200
prove that the angle bisectors of a triangle are concurrent. Given segment DB bisects angle ABC, and segment EC bisects angle ACB.
since F is on the bisector of angle ABC, it's equidistant from AB and BC. since it's also on the angle bisector of angle ACB, it's also equidistant from AC and BC. Therefore, I is equidistant from all three sides of the triangle.
200
the circumference of a circle is 32pi. find the radius
what is "16"
C/d=pi and C=32pi.so d=32. r=16
200
- The lengths of the sides of a triangle are x, 16 and 31, where x is the shortest side. If the triangle is not isosceles, what is a possible value of x?
By the triangle rule, x lies between 31 – 16 = 15 and 31 + 16 = 47. That is, we have 15 < x < 47. But we are also given that x is the length of the shortest side of the triangle. So x < 16.Therefore the answer is any number between 15 and 16.
200
Given
in a quadrilateral, its angles measure to be
<A=3x+9
<B=5x+20
<C=3x
<D=2x+6
Find <D
56
200
why does ∠1 = ∠4 given that m and n are parallel lines?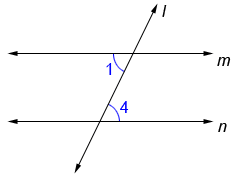 
∠1 and ∠4 are alternate interior angles, which makes them equivalent
300
the angle bisectors of triangle ABC are perpendicular segments from G to the sides of the triangle. why is GE=GD=GF?
since G is th equidistant from the sides of triangle ABC, then GE=GD=GF
300
The length of a 73 degree arc of a circle is 15. What is the circumference of the circle?
what is "75"
a 72 degree arc is 72/360=1/5 of an entire circle. since this arc has length 15, the entire circumference of the circle has length 5(15)=75
300
Three fair coins are tossed at the same time. What is the probability that all three coins will come up heads OR all will come up tails?
1/4. 1/8 (all heads) + 1/8 (all tails) = 1/4.
300
Given:
Trapezoid (not isosceles)
COCO WILL DRAW THIS ON THE BOARD
find: a triangle equal in area to ABD
ACD
300
find the length of AB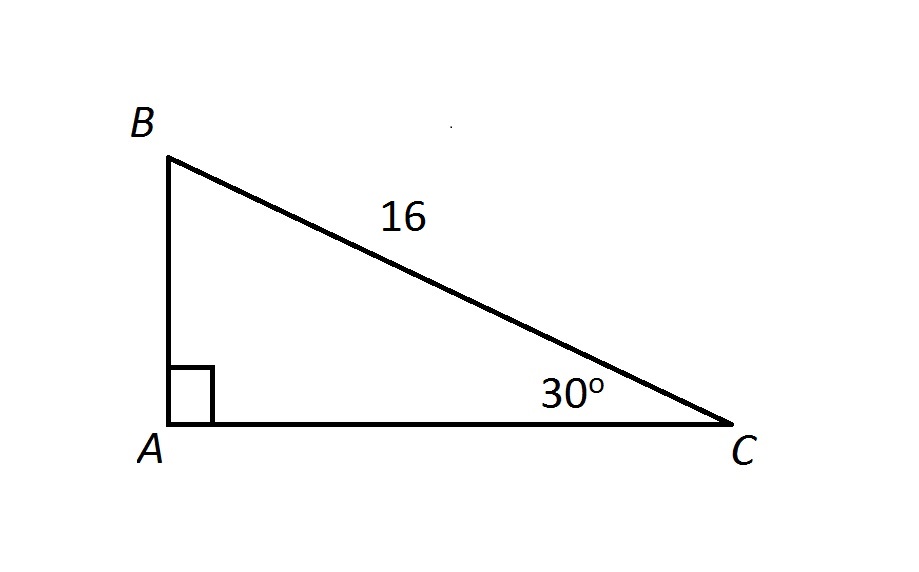 
8
400
Anna and Betty are 180 yards apart, at points A and B in the diagram, respectively. There is a semi-circular path from Anna to Betty. Chuck is at point C, the midpoint of this path. Anna must walk to Chuck and then to Betty. How much farther must Anna walk if she follows the path if she "cuts across", walking straight to C then straight to B?
what is "90pi-180sqrt2 yards"
triangle ACB is a 45-45-90 triangle
alt:
connect C to center of circle, O. since arc AC=arc CB=90 degrees, angle AOC=COB=90. segment OA, OB, and OC are all radii of the circle, so triangle AOC and BOC are 45-45-90 triangles. since AB=180 yards, we have AO=OB=OC=180/2=90 yards and AC=BC=COsqrt2 = 90 sqrt2 yards. Since arc AB is 1/2 a circle, its length is (AB)pi/2=90pi yards. So, Anna must walk 90pi- (AC+BC)=90pi-180sqrt2 yards farter if she follows the path
400
Chord YZ of a circle with center O has length 12. The circumference of the circle is 24pi. What kind of triangle is YOZ? What is the radius of the circle? Find the length of arcYZ
To find the length of the arc, we must find angle YOZ. We start by figuring out lengths. Since circumference is 24pi, the diameter is 24 and radius is 12. Hence, OY=YZ=ZO, so triangle YOZ is equilateral. therefore, angle YOZ is 60 degrees, and our arc is 1/6 of the circle. the length of arc YZ is (1/6)(24pi)=4pi
400
in triangle ABC, AB, BC, and AC are tangent to the circle with center r. given that angle BAC=70 and BCA=50. what is the measurement of angles RCA and ARC
because the circle is tangent to all three sides of triangle ABC, it's the incircle of triangle ABC. therefore, r is the incenter of triangle ABC, and rC and RA are angle bisectors of angles BAC and BCA, respectively.
400
what is the area of a circle in which a 3x4 rectangle is inscribed?
25pi. The length of a diagonal of a 6 by 8 rectangle is 10 (pythagorean theorem). The diagonal of the rectangle is the diameter of the circle inscribed, and A = pi*r^2
400
find the value of ∠QPM 
32°
500
prove heron's formula
y=a-x
apply the pythagorean theroem to triangles ABX and ACX, then subtract the second equation from thefirst to find x.
x^2+h^2=c^2
h^2=c^2-x^2
apply expression from earlier into the h^2 equation. solve.
s is the semiperimeter, 2s=a+b+c.
500
Chords AB and CD of circle O have the same length. arc AB=arc CD. prove that AB=CD
form two triangles by conecting A, B, C, and D to O. Since AB=CD, AO=CO, and BO=DO, we have triangel ABO similar to triangle CDO by SSS. Therefore, angle AOB=angle COD, so arcs AB and CD are congruent
500
Fruit for a dessert costs $1.20 a pound. If 5 pounds of fruit are needed to make a dessert that serves 18 people, what is the cost of the fruit needed to make enough of the same dessert to serve 24 people?
$8.00. If 5 pounds of fruit serve 18 people, then 5/18 pound serves one person, so 24 x 5/18 = 20/3 pounds. Since the fruit costs $1.20 a pound, the cost of the fruit needed to serve 24 people is 20/3 x $1.20 = $8.00.
500
What is the number of sides of a polygon in which the sum of the degree measures of the interior angles is 4 times the sum of the degree measures of the exterior angles?
Sum of the degree measures of exterior angles is 360. S = (n-2)180 = 4 x 360, where n=number of sides. Solving for (n-2) = 8 or n=10.
500
find ∠ABC 
38.4°