1: Tools of Geometry
2: Reasoning and Proof
3: Parallel and Perpendicular Lines
4: Triangles
5: More about Triangles
100
Name a polygon that is always regular and a polygon that is sometimes regular.
Always regular: square
Sometimes regular: rectangle
Teacher will check for answers.
100
Compare conjunction and disjunction.
Conjunction: and (both must be true)
Disjunction: or (either can be true)
100
Compare the slope of:
1. Two parallel lines
2. Two perpendicular lines
1. Same slope
2. Opposite reciprocal
100
Sometimes, always, never: A triangle has multiple obtuse angles.
Never
100
What is the vocabulary for the point shown?
Circumcenter (the lines are perpendicular bisectors)
200
Sometimes, always, never: The sum of two acute angles is an obtuse angle.
Sometimes
200
What property justifies this statement?
If 7(x-3) = 35, then 35 = 7(x-3).
Symmetric property
200
Draw and label one pair of each on the same diagram: alternate interior, alternate exterior, corresponding, consecutive interior
Teacher will check for answers
200
True or false: An equiangular triangle must also be equilateral.
False
200
If G is the centroid of triangle ABC and GF = 4. Find the length of GC.
GC = 4*2 = 8
300
Find the volume of a cube that has a total surface area of 54 square millimeters.
surface area = 6s2 = 54
s = 3
volume = s3 = 27 cube millimeters
300
Two supplementary angles always form a linear pair. What is a counterexample to this statement?
Two nonadjacent supplementary angles
300
Find the distance between these two parallel lines:
y = x - 11
y = x -7
4
300
Find the values of x and y.
x = 3 (x + 1) = 4
y = 4 --> KNL is equiangular
300
SR = ?
SR = 15
400
The length of each side of a cube is multiplied by 5. What is the change in the volume of the cube?
The volume will be 125 (53) times greater.
400
What is the contrapositive to this statement?
If a triangle has one obtuse angle, then it is an obtuse triangle.
If a triangle is not an obtuse triangle, then it does not have one obtuse angle.
400
Find the the measure of angle d.
180 - 45 = 35
400
What information do you need to prove these two triangles congruent by AAS?
Angle G is congruent to Angle P
400
In ΔDOG, point C lies on the side of the triangle between points D and O. DG = 5, GO = 12, and DC = 3. What is the range of possible values for CO?
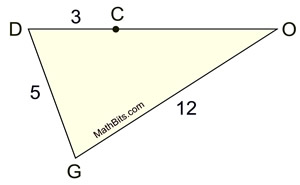
7 < CO < 14
500
Alex and Emily are calculating the surface area of a rectangular prism with dimensions 5 in, 3 in, and 4 in. Is either correct?
Alex: (5*3) * 6 faces = 90 in2
Emily: (2*5*4*3) = 120 in2
Neither is correct:
2(5*4) + 2(5*3) + 2(3*4) = 94 in2
500
p: A plane contains at least three noncollinear points.
q: A square yard is equivalent to three square feet.
r: The sum of the measures of two complementary
angles is 180.
Write the compound statement for: p ∧ ~r.
A plane contains at least three noncollinear points, and the sum of the measures of two complementary angles is not 180.
True.
500
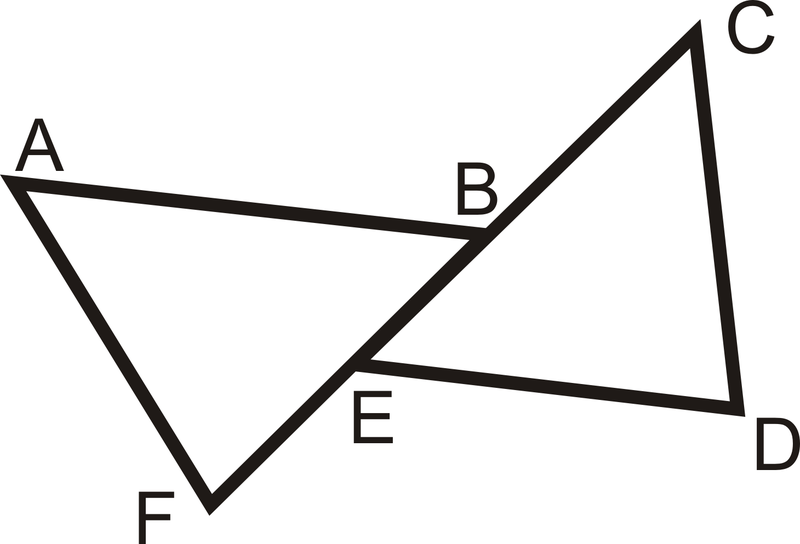
If angles 4 and 6 are congruent, which two lines must be parallel?
Lines y and z by alternate interior angles.
500
Given that lines AB and ED are parallel, angles C and F are congruent, and lines AB and ED are congruent, what justification would you use to prove that lines AF and CD are congruent?
Angles ABE and DEB are congruent - Alternate interior angles theorem
Triangles ABF and DEC are congruent by ASA
Lines AF and CD are congruent - corresponding parts of congruent triangles
500
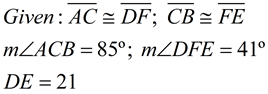
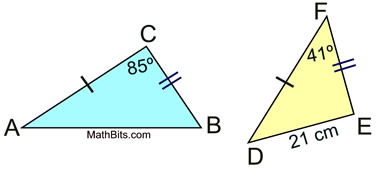Find the range of possible values for AB.
AB > 21.