Tools of Geometry
Reasoning and Proof
Parallel and Perpendicular Lines
Congruence
Similarity
Relationships in Triangles
200
The name of this postulate, if A, B, and C are collinear:
m\bar(AB)+m\bar(BC)=m\bar(AC)
What is the segment addition postulate?
200
To prove angles congruent, they must have the same this.
What is measure?
200
If same-side interior angles are supplementary, then the lines forming those angles from the transversal are this.
What is parallel?
200
If triangle LMN is congruent to triangle OPQ, then angle MLN is congruent to this angle.
What is angle POQ?
200
Solve the proportion:
(x+8)/10=2/x
What is x=-10 and x=2?
200
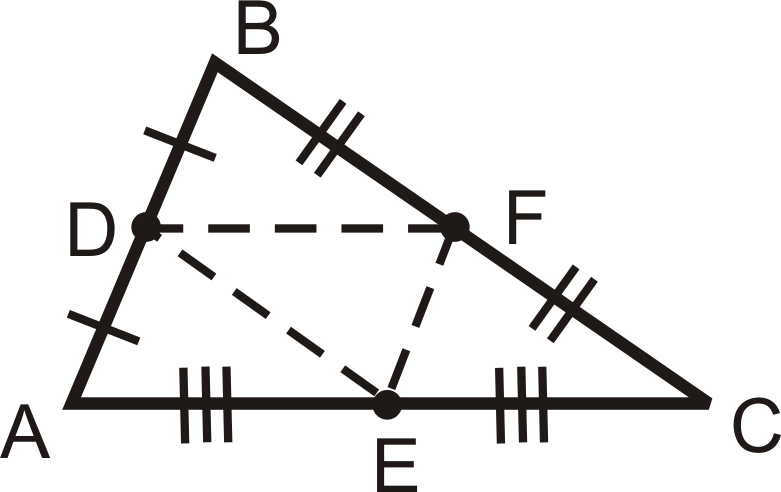
The lines shown here.
What are midsegments?
400
Three noncollinear points create this kind of geometric construction, not to be confused with one in the sky.
What is a plane?
400
This step of reasoning in a proof allows us to say something is congruent to itself.
What is the reflexive property (of Congruence)?
400
Find the values of x and y.
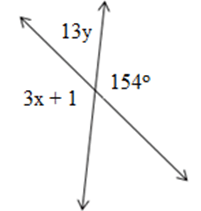
What is x=51 and y=2?
400
State what additional information is needed to prove these triangle congruent by the HL Theorem.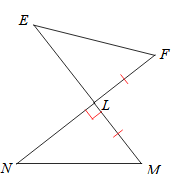
What is
\bar(EF)\cong\bar(NM)?
400
If the similarity and perimeter ratio are 4:9, then the area ratio is this.
What is 16:81?
400
State if the following three sides can form the sides of a triangle. Show justification for your answer.
15, 17, 32
No, 15+17=32, but the two smaller sides should add to be greater than the largest side.
600
Find the midpoint of AB given A(2, 9) and B(–10, 7).
What is (-4, 8)?
600
Give the contrapositive of the following statement:
If the sky is blue, then the grass is green.
What is:
If the grass is not green, then the sky is not blue.
600
Write an equation in slope-intercept form for the line perpendicular to y = 3x – 7 through the point (-6, 12).
What is
y=-1/3x+10?
600
The formula 180(n-2), given for finding the total angle measure within a polygon, can be converted into
(180(n-2))/n
for these kinds of polygons to determine the measure of each individual angle.
What are regular polygons?
600
Ray LO bisects angle NLM, LM = 45, NO = 18, and OM = 27. Find LN.
What is LN=30?
600
If a point is on the perpendicular bisector of a segment, then that point is this from the endpoints of the segment.
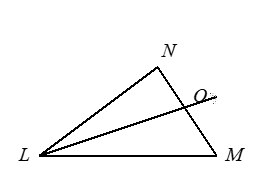
What is equidistant?
800
Find the distance between points S(4, 9) and T(2, 4) to the nearest tenth.
What is 5.4?
800
Give the biconditional of the following statement:
If you are from Indiana, then you are a Hoosier.
What is:
You are from Indiana if and only if (iff) you are a Hoosier?
800
Let the measure of angle 3 be 137 degrees. Find the measures of the other three angles.
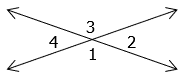
What is
m\angle 1=137, m\angle 2=m\angle 4=43?
800
The only theorem of our 3-letter abbreviations for triangle congruence, this one uses the interior angle sum to become ASA triangle congruence.
What is AAS or SAA triangle congruence?
800
Solve for x.
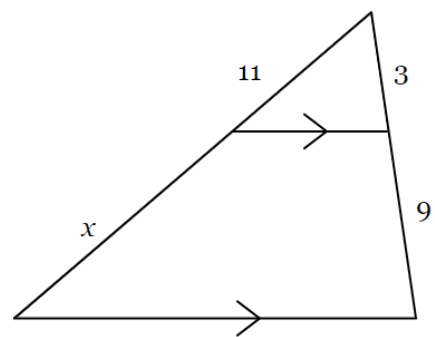
What is x=33?
800
A triangle has side lengths 8 and 9 cm. Find the range of possibilities of the third side.
What is 1cm<x<17cm?
1000
Write an equation for the vertical line that contains point E(7, –9).
What is x=7?
1000
If the two angles shown below add up to 90 degrees, we use this term to describe the two angles together.
What is complementary?
1000
In any given polygon, the exterior angles add to this sum.
What is 360 degrees?
1000
Write a two-column proof for the following problem:
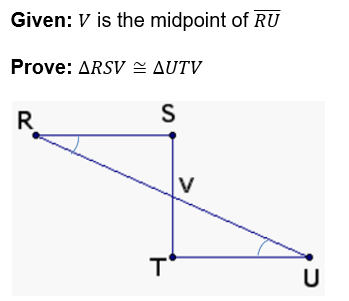
1. V is the midpoint of
\bar(RU)
1. Given
2.
\bar(RV)\cong\bar(UV)
2. Definition of Midpoint
3.
\angleR\cong\angleU
3. Given
4.
\angleRVS\cong\angleUVT
4. Vertical Angles Theorem
5.
\DeltaRSV\cong\DeltaUTV
5. ASA
1000
Solve for x. Leave in simplest radical form.
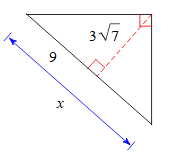
What is
x=16
1000
Solve for x.
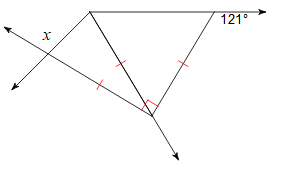
What is x=104 degrees?