Net
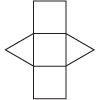
a two-dimensional representation or pattern for a three-dimensional object
Edge
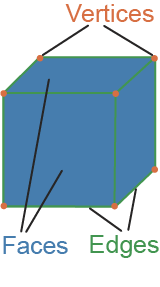
where these faces meet
Diameter of a Circle
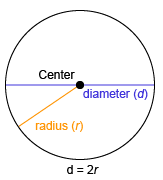
the length of a segment that goes from one point on a circle through its center, and continues on to another point on the other side of the circle
Kite
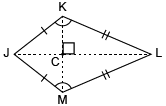
Quadrilateral with two pairs of congruent sides that are adjacent to each other.
Exterior Angle of a Polygon
What is the measure of an exterior angle of a 12-sided regular polygon?
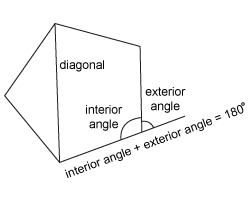
The angle between a side and an adjacent side extended, on the exterior of a closed shape
30˚
The sum of the measure of the exterior angles is always 360°. Since there are 12 exterior angles, one at each vertex, \frac{360}{12}=30˚12360=30˚.
Secant
a line cutting through two points on a circle, an extended chord
Diagonal
on a polygon, a line segment drawn from one vertice to another that is NOT a side
Tangent
a line that touches the circle at one point ONLY
Inscribed Angle
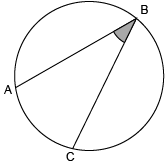
an angle made from points on a circle's circumference
Example.
In the image, ∠ABC
Polygon
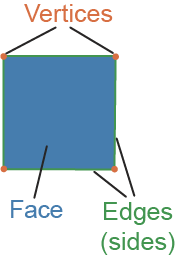
a multi-sided, closed figure made up of vertices (corners) and edges (sides)
Radius of a Circle
the distance from the center of a circle to a point on the circle
Circumcircle
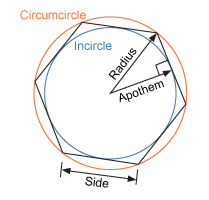
a circle drawn on the outside of a polygon that connects all the vertices
Incircle

a circle drawn on the inside of the polygon that touches the midpoint of each side
Apothem

a line segment from the center of the polygon to the midpoint of a side
Lateral Surface Area
The sum of the areas of all faces excluding the base(s) of a solid object
Example.
For a soup can, the area of the curved part (what is normally covered by the label)
In the evening, a room-parent baked a two-layer cake for his child to take to class the next day. The cake had a height h of 22 cm and a radius r of 14 cm. In the morning, a wedge was missing from the cake, as shown. If the arc-length s of the missing wedge was 7 cm, which of the following is the best approximation of the volume of the missing wedge?
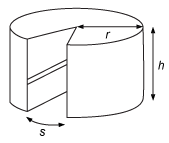
1100 cm3
The wedge is a prism with a base (the sector that was removed) and a height (of the overall cake). Therefore, the total volume is the area of the sector times the height of the cake.
To find the area of the sector, multiply the area of the base of the whole cake by the ratio of the arc length over the circumference: A_{sector}= \pi r^{2} \left( \frac{s}{2 \pi r} \right) =\frac{rs}{2}=\frac{ \left( 14 \text{ cm} \right) \left( 7 \text{ cm} \right) }{2}=49 \text{ cm}^2Asector=πr2(2πrs)=2rs=2(14 cm)(7 cm)=49 cm2.
The volume of the missing wedge is V=A_{sector}h = \left( 49 \text{ cm}^{2} \right) \left( 22 \text{ cm} \right) =1078 \text{ cm}^{3} \approx 1100 \text{ cm}^{3}V=Asectorh=(49 cm2)(22 cm)=1078 cm3≈1100 cm3.
Convex Polygon
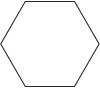
polygon for which all interior angles are less than 180⁰; vertices seem to point outward; all diagonals will be contained within the polygon
Equiangular Polygon
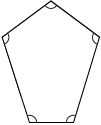
polygon with all angles congruent (equal measure)
Radius (of a Polygon)

a line segment from the center of the polygon to a vertice
Irregular Polygon
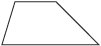
A polygon with sides and angle measures that are not all the same
Which of the following terms would be used to describe a polygon with six sides whose angles are all of equal measure?
A. an irregular quadrilateral
B. a regular octagon
C. an irregular pentagon
D. a regular hexagon
D. a regular hexagon
Since all angles are of equal measure, the polygon is regular. Since it has six sides it is a hexagon.

The side lengths of parallelogram X are 2 and 3. A similar parallelogram Y has side lengths 10 and 15. The area of parallelogram Y is how many times the area of parallelogram X?
25
The ratio of the sides of the two parallelograms is 5:1. The ratio of the areas is the square of the ratio of the sides, or 25:1. Parallelogram Y has an area 25 times that of X.
What is the area of the equilateral triangle ABC?
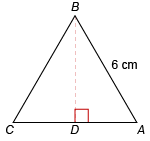
A = 9√3 cm²
Since triangle ABC is equilateral, all sides are congruent, and all angles are congruent and equal 60°. This makes triangle ADB a 60-30 right triangle. Since the hypotenuse is 6 cm, DA is 3 cm, and the height of the triangle, BD, is 3√3. The area of triangle ABC is A = ½bh = ½(6)(3√3) = 9√3. (Note: An alternate formula for the area of equilateral triangles is A = [(s²√3)/4] , where s = side length. The side of the given triangle is 6 cm, so A = [(6²√3)/4] =[(36√3)/4] = 9√3 cm².)
Kellie is redecorating her bedroom. She wants to paint her bedroom door green but needs to know how much paint to buy. If one quart of paint can cover 15,000 cm2, how many quarts of paint will Kellie need?
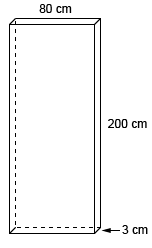
3
First, find the surface area of the door.
2(80\times 3)+2(80\times 200)+2(200\times 3)=480+32000+1200=33,680 \text{ }cm^{2}2(80×3)+2(80×200)+2(200×3)=480+32000+1200=33,680 cm2
If each quart of paint can cover 15,000 cm2, Kellie will need \frac{33,680 \text{ }cm^{2}}{15000\text{ }cm^{2}}=2.2515000 cm233,680 cm2=2.25 quarts to paint her door. This number must be rounded up to 33 since paint must be purchased in whole number increments.
A right cylinder has a height of 10" and a base with a circumference of 12π". What is the surface area?
192π in²
SA = 2πr² + Ch = 2 πr². If the circumference is 12π, then 2πr = 12π and r = 6. Since r = 6 and h = 10, substitute these values into the equation for finding SA. SA = 2π6² + 12π(10) = 72π + 120π= 192π².