IF ST = 17 and RT = 38, find RS.

21
A is the midpoint of line XT. Find AY and XY.
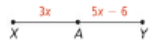
AY = 9
XY = 18
Name a pair of adjacent angles. Then name a pair of vertical angles.
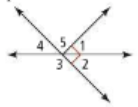
Answer may vary.
Segment RS has endpoints at (2,4) and (-1,7). What are the coordinates of its midpoint M?
(0.5,5.5)
Find the distance between points (10,14) and (-8,14).
18
Find the length of CE using the distance formula.
6
Find the value of PT if PT= 7x-24 and TQ = 6x-2.

130
Name an angle supplementary to <AOD. Then name an angle complementary to <EOD.
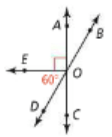
Supplementary to <AOD: <DOC or <AOB
Complementary to <EOD: <DOC
The midpoint of segment BC is (5,-2). One endpoint is (3,4). What are the coordinates of the other endpoint?
(7,-8)
Find the area of the rectangle with a base of 40 cm and height of 2 m.
8,000 cm^2 or 0.8 m^2
What are two other ways to name plane C?
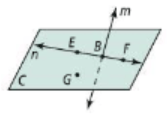
Answer may vary.
Name 4 ways to name this angle.
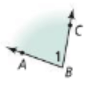
<ABC, <CBA, <B, <1
Ray GH bisects <FGI. Solve for x and find m<FGH.
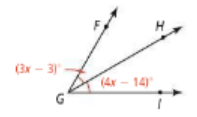
x=11
m<FGH = 30
Find the distance between points (-9,8) and (-6,0).
sqrt73 or 8.5 units
Can you make the conclusion that C is the midpoint of line JD.
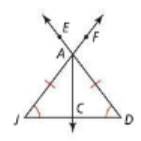
No
Name the pair of opposite rays with endpoint S.
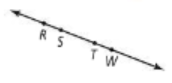
Ray SR and Ray SW
If m,ABD = 79, what are m<ABC and m<DBC?
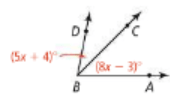
m<ABC = 45
m<DBC = 34
What is a perpendicular bisector?
A line, segment, or ray that is perpendicular to the segment at its midpoint.
Find the perimeter and area of a rectangle with base 3 in and height 7 inch.
P = 20 in
A = 21 in^2
Find the area of the shaded region. All angles are right angles.
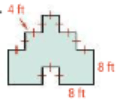
208 ft^2
Name two planes that intersect on line TX.
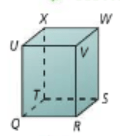
Plane QUXT and plane XWST
Solve for x. Find the angle measures. m<AOB = 4x-2, m<BOC = 5x+10, m<COD = 2x+14.
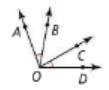
x = 8
m<AOB = 30
m<BOC = 50
m<COD = 30
Name the steps in constructing congruent segments.
Step 1: Draw a ray.
Step 2: Open the compass to length of line AB.
Step 3: With the same compass setting, put the compass point on point C. Draw an arc that intersects the ray. Label the point of intersection D.
Find the circumference and area of a circle with d = 7.3 m.
C = 22.9 m
A = 41.9 m^2
Construct a congruent angle to angle A.

2 arcs.