Conditional Statements
Properties
Types of Angles
Proofs
100
Name the Hypothesis in this conditional statement:
If something is a bird, then it can fly
What is if something is a bird?
100
The name of this property
If a = b, then a + c = b + c
What is the addition property of equality?
100
What is adjacent angles?
100
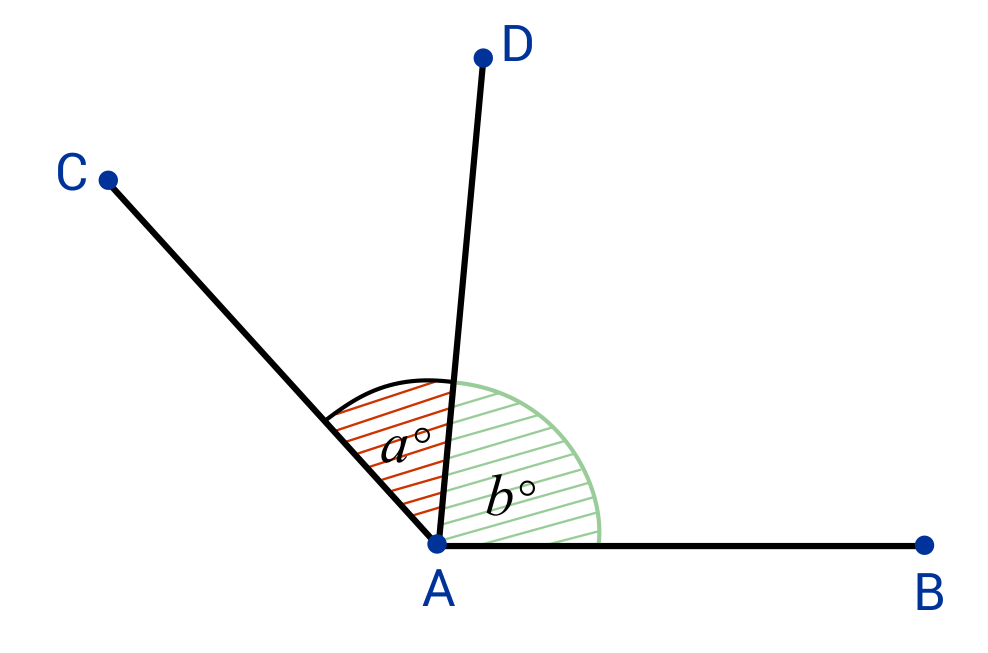
Find 1a. ________
What is ∠1 and ∠2 are supplementary, and ∠2 and ∠3 are supplementary?
200
Name the Conclusion in this conditional statement:
If something is a bird, then it can fly
What is, then it can fly
200
The name of this property:
If a = b and c does not =0, then a/c=b/c
What is the division property of equality?
200
What is supplementary angles?
200
Find 3b. ________
m∠1 + m∠2 = m∠2+ m∠3
300
State the converse of the conditional:
If two angles are supplements, then their sum equals 180.
What is, if two angles sum equals 180, then they are supplements?
300
The name of this property:
a(b+c) = ab + ac
What is the distributive property?
300
Two pairs of congruent angles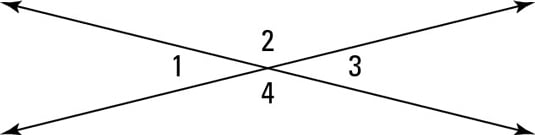 
What is ∠1 ≅ ∠3 and ∠2 ≅ ∠4?
300
Find 5c. ________
What is the transitive property of equality?
400
When a conditional and converse are true, you can combine them into ________ using the phrase _______
What is biconditional and if and only if?
400
The property used in:
If m∠A = m∠B, then m∠B = m∠A
What is the symmetric property of equality?
400
Theorem 2-3: If two angles are complements of the same angle, then ______________
What is, the two angles are congruent?
400
Find 6d. _________
What is ∠1 ≅ ∠3?
500
The biconditional of these conditional statements:
If the tea kettle is whistling, the water is boiling
If the water is boiling, then the tea kettle is whistling
What is, the tea kettle is whistling if and only if the water is boiling?
500
The property used:
If ∠A ≅ ∠B and ∠B ≅ ∠C, then ∠A ≅ ∠C
What is the transitive property of congruence
500
Theorem 2-5: If two angles are congruent and supplementary, then _______________
What is, each is a right angle?