Angle Pair Relationships
Basic Vocab
Proofs
Parallel/Perpendicular Lines
Theorems
100
Solve for x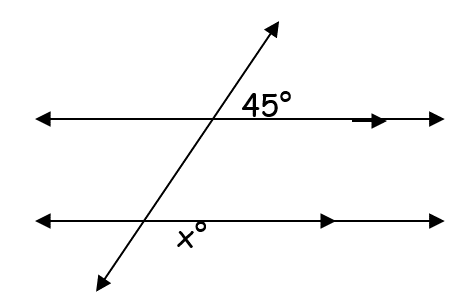
135°
100
Given the rectangular prism, are EF and AE parallel, perpendicular or skew?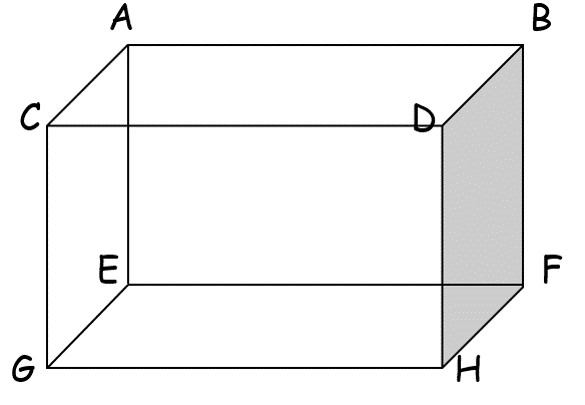
Perpendicular
100
What is the reason for statement #3
Alternate exterior angles theorem
100
What is the slope of a line parallel to the line y=2x-5
2
100
What theorem proves this statement true?
If m<4 = m<6, then l is parallel to m.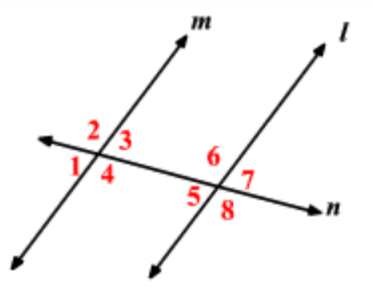
Converse of alternate interior angles theorem
200
Solve for x
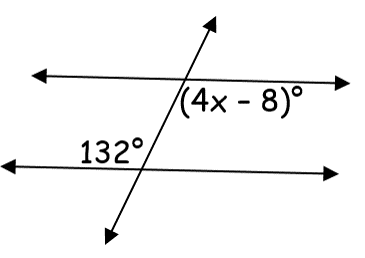
x = 35
200
What angle is same side interior to <6?
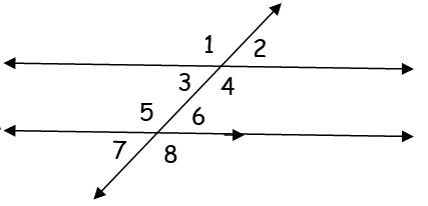
<4
200
What is the reason for statement #5?
Transitive Property
200
What is the slope of a line perpendicular to the line
y= 2/3 x+2
-3/2
200
What theorem proves this statement?
If lines l and m are parallel, then angles 2 and 7 are congruent.
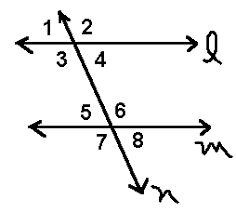
Alternate Exterior angles theorem
300
Solve for x and y
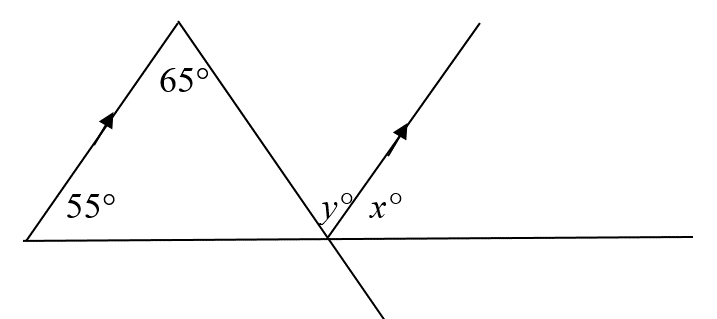
x= 55°, y= 65°
300
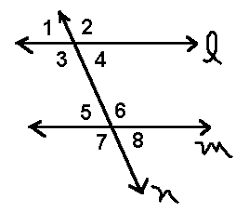
What type of angles are <3 and <6?
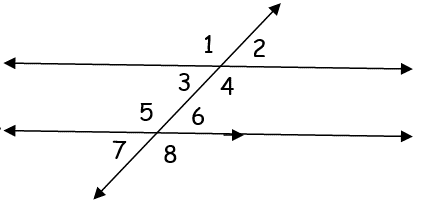
Alternate Interior Angles
300
What is the statement and reason for step #4?
<6cong<11,
Alternate Exterior Angles Theorem
300
Write the equation of a line that passes through the point (-7, -1) and is parallel to y = 2x - 11.
y=2x+13
300
What theorem proves this statement?
If lines l and m are parallel, then angles 3 and 5 are supplementary.
Same-side interior angles theorem
400
Solve for x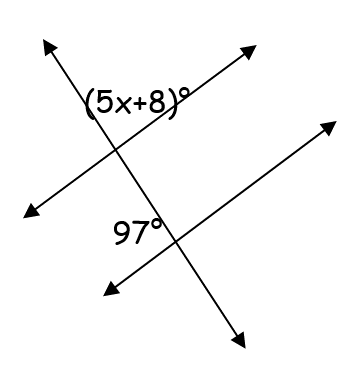
x = 15
400
In the rectangular prism, name a plane parallel to ACGE.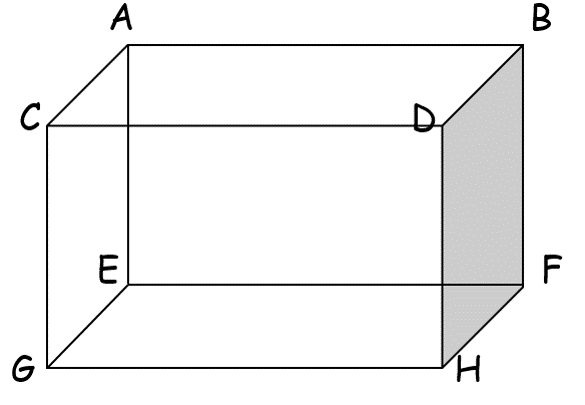
Plane DBFH
400
Write the reasons for all the statements
1. & 2. Given
3.Corresponding Angles Post.
4. Alternate interior angles theorem
5. Transitive property
400
Are the following lines parallel, perpendicular or neither?
(y - 5)=-2(x+3)
y=1/2x+11
Perpendicular. (Slopes are opposite reciprocals.)
400
What theorem proves this statement?
If angles 1 and 5 are congruent, then lines l and m are parallel.
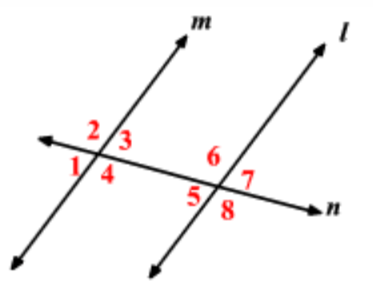
Converse of the corresponding angles postulate.
500
Solve for x and y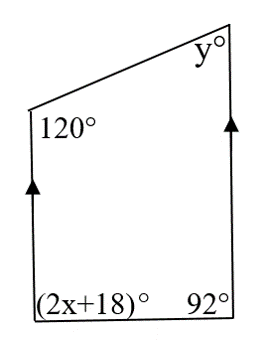
x=35, y=60
500
Name all angles supplementary to <5
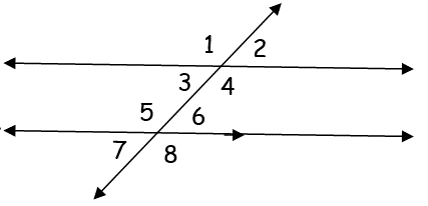
<6, <7, <3, <2
500
Complete the proof
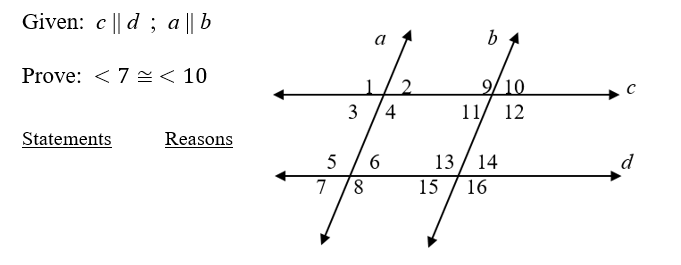
1. c ll d and a ll b 1. Given
2. <7 cong<15 2. Corr. angles post.
3. <15 cong<14 3. Vertical <'s Thrm
4. <14 cong<10 4. Corr. angles post.
5. <7 cong<10 2. Transitive Prop.
500
Are the following lines parallel, perpendicular or neither? Line AB goes through A (-2, 6) and B (5, -1) and line CD goes through C (9, -2) and D (1, 7).
Neither. (The slopes of -1 and -9/8 aren't a special relationship.)
500
What theorem justifies that angle 1 is congruent to angle 4?
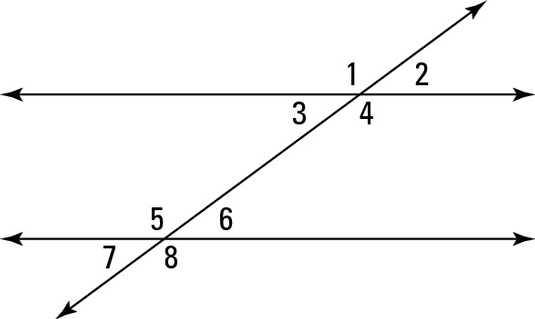
Vertical angles theorem