Scale Factor
Similar Polygons
Proving Triangles Similar by AA
Proving Similarity by SSS and SAS
Proportionality Theorems
100
Find the Scale Factor
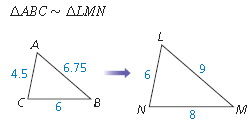
3/2
100
The polygons are similar. Find the value of x.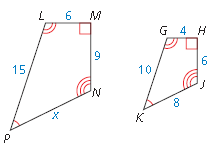
x = 12
100
Determine whether the triangles are similar. If they are, write a similarity statement. SHOW WORK.
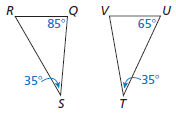
no; m∠R = 60°
100
Determine whether △JKL or △RST is similar to △ABC.
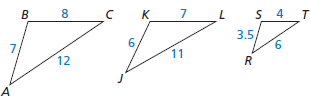
△RST
100
Find the length of AB
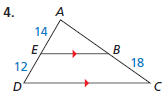
AB = 21
200
Find the Scale Factor.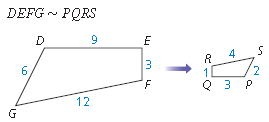
1/3
200
The polygons are similar. Find the value of x.
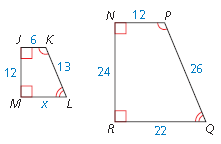
x = 11
200
Determine whether the triangles are similar. If they are, write a similarity statement. SHOW WORK.
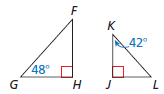
yes; ∠H ≅ ∠J and ∠F ≅ ∠K, so △FGH ∼ △KLJ.
200
In Exercises 5 and 6, fi nd the value of x that makes △DEF ∼ △XYZ.
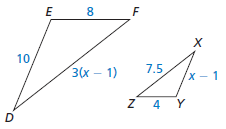
x = 6
200
Determine whether KM || JN.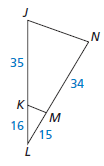
NO
300
Find the scale factor.
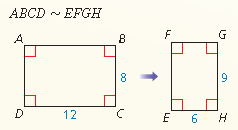
3/4 or 0.75
300
The polygons are similar. Find the values of x and y.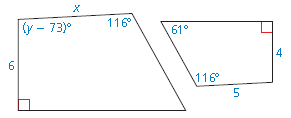
x = 7.5, y = 166
300
Show that the two triangles are similar.
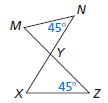
∠N ≅ ∠Z and ∠MYN ≅ ∠XYZ (vertical angles), so △MYN ∼ △XYZ.
300
Verify that △ABC ∼ △DEF. Find the scale factor of △ABC to △DEF.
△ABC: BC = 18, AB = 15, AC = 12
△DEF: EF = 12, DE = 10, DF = 8
300
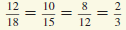
Find the length of VX.
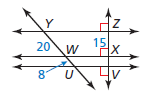
VX = 6
400
The polygons are similar. The area of one polygon is given. Find the area of the other polygon.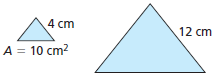
Area = 90 square cm
400
The polygons are similar. Find the values of x and y.
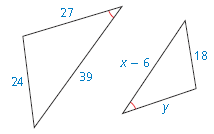
x = 35.25, y = 20.25
400
Show that the two triangles are similar.
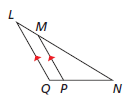
∠Q ≅ ∠MPN (corresponding angles) and ∠N ≅ ∠N, so △LNQ ∼ △MNP.
400
Sow that the triangles are similar and write a similarity statement. Explain our reasoning.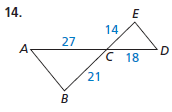
∠ACB ≅ ∠DCE and CE/CB = DC/AC, so △ABC ∼ △DEC.
400
Find the value of the variable.
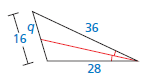
q = 9
500
The polygons are similar. The area of one polygon is given. Find the area of the other polygon.
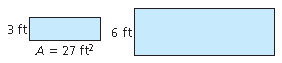
108 Square Feet
500
In table tennis, the table is a rectangle 9 feet long and 5 feet wide. A tennis court is a rectangle 78 feet long and 36 feet wide. Are the two surfaces similar? Explain. If so, find the scale factor of the tennis court to the table.
no; Corresponding side lengths are not proportional.
500
A flagpole casts a shadow that is 50 feet long. At the same time, a woman standing nearby who is 5 feet 4 inches tall casts a shadow that is 40 inches long. How tall is the flagpole to the nearest foot?
You can use a proportion to fi nd the height x. Write 5 feet 4 inches as 64 inches so that you can form two ratios of feet to inches.
x ft / 64 in. = 50 ft / 40 in.
Write proportion of side lengths.
40x = 3200 Cross Products Property
x = 80 Solve for x.
The flagpole is 80 feet tall.
500
Certain sections of stained glass are sold in triangular, beveled pieces. Which of the three beveled pieces, if any, are similar?
The pieces with side lengths of 5.25 inches and 7 inches (blue and red)
500
In a perspective drawing, lines that are parallel in real life must
meet at a vanishing point on the horizon. To make the train cars
in the drawing appear equal in length, they are drawn so that the
lines connecting the opposite corners of each car are parallel.
Find the length of the bottom edge of the drawing of Car 2.
The length of car 2 is approximately 4.3 cm in the drawing.