Vocabulary
Similar Polygons
Proving Triangles Similar
Proving Quadrilaterals
Mixed Theorems
100
Any parallelogram with 4 right angles.
Square and Rectangle
100
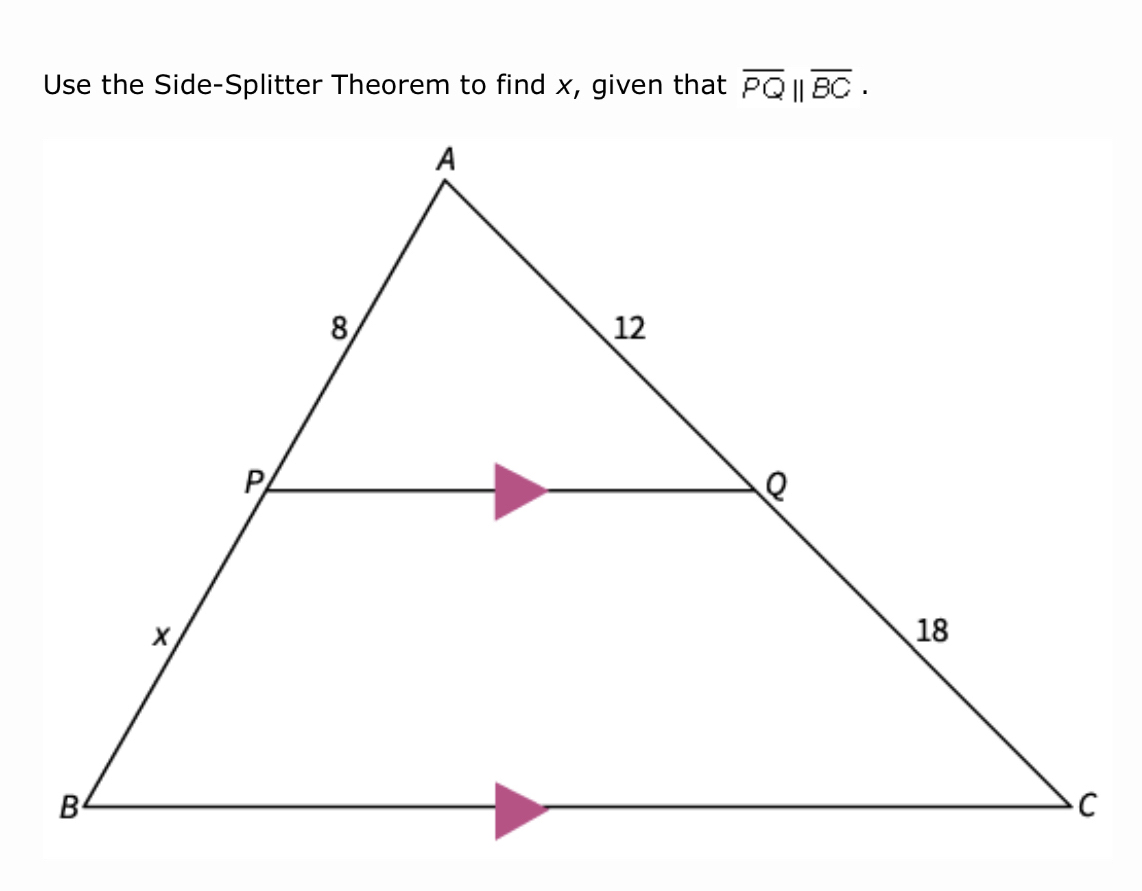
The polygons are similar. Find the value of x.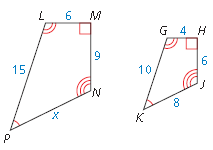
x = 12
100
Determine whether the triangles are similar. If they are, write a similarity statement. SHOW WORK.
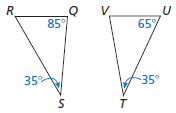
no; m∠R = 60°
100
Name all the possible quadrilaterals that the statement is true for:
Diagonals are congruent
Rectangle & Square
100
Determine whether △JKL or △RST is similar to △ABC.
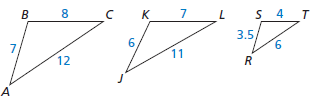
△RST
200
A quadrilateral with 1 pair of parallel sides, 1 pair of equal sides, and no right angles
Trapezoid
200
The polygons are similar. Find the value of x.
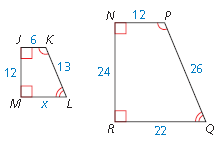
x = 11
200
Determine whether the triangles are similar. If they are, write a similarity statement. SHOW WORK.
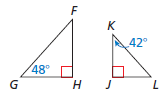
yes; ∠H ≅ ∠J and ∠F ≅ ∠K, so △FGH ∼ △KLJ.
200
Prove that the following points represent the vertices of a parallelogram:
A: ( 2 , 4 ) , B: ( 4 , -3 ) , C: ( 9 , -6 ) , D: ( 7 , 1 )
slope of AB & CD = -7/2
slope of BC & AD = -3/5
measure of AB & CD = root 53
measure of BC & AD = root 34
200
x = 12
300
Which statement is true? A) A trapezoid has 2 pairs of parallel sides. B) A parallelogram has 2 pairs of parallel sides. C) A Square has only 2 right angles. D) A rectangle has only 5 sides.
B) A parallelogram has 2 pairs of parallel sides.
300
The polygons are similar. Find the values of x and y.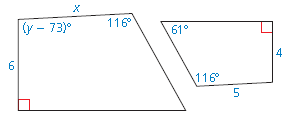
x = 7.5, y = 166
300
Show that the two triangles are similar.
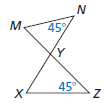
∠N ≅ ∠Z and ∠MYN ≅ ∠XYZ (vertical angles), so △MYN ∼ △XYZ.
300
Name all the possible quadrilaterals that the statement is true for:
Opposite sides are parallel
Parallelogram, Rhombus, Rectangle, & Square
300
DE || AC
Find AB
AB= 44.8
400
This is a correct similarity statement for these two triangles.
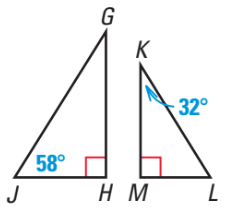
What is
△JGH~△LKM?
400
The polygons are similar. Find the values of x and y.
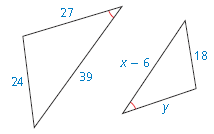
x = 35.25, y = 20.25
400
Show that the two triangles are similar.
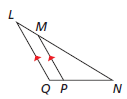
∠Q ≅ ∠MPN (corresponding angles) and ∠N ≅ ∠N, so △LNQ ∼ △MNP.
400
Prove that the following points represent the vertices of a parallelogram:
M: ( -7 , -3 ) , N: ( 6 , 10 ) , P: ( 8 , 4 ) , Q: ( -5 , -9 )
slope of MN & PQ = 1
slope of NP & MQ = -3
measure of MN & PQ = 13root 2
measure of NP & MQ = 2 root 10
400
In Exercises 5 and 6, fi nd the value of x that makes △DEF ∼ △XYZ.
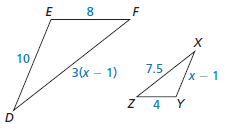
x = 6
500
A quadrilateral with 2 pairs of parallel sides and 4 equal sides, but no right angles
Rhombus
500
In a perspective drawing, lines that are parallel in real life must
meet at a vanishing point on the horizon. To make the train cars
in the drawing appear equal in length, they are drawn so that the
lines connecting the opposite corners of each car are parallel.
Find the length of the bottom edge of the drawing of Car 2.
The length of car 2 is approximately 4.3 cm in the drawing.
500
Sow that the triangles are similar and write a similarity statement. Explain our reasoning.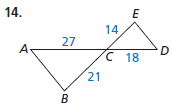
∠ACB ≅ ∠DCE and CE/CB = DC/AC, so △ABC ∼ △DEC.
500
In the diagram VWXY is a parallelogram, complete each statement
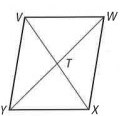
<VYX is supplementary to ?
<VYX is supplementary to <WVY & <WXY
500
How tall is the person? (feet, inches)
4 feet 4 inches