Unit 1: Intro to Logic and Euclidean Geometry
Unit 2: Coordinate Geometry and Transformations
Unit 3: Relationships of Lines and Transversals
Unit 4A: Relationships in Triangles
Unit 4B: Similarity
100
Name a point collinear to V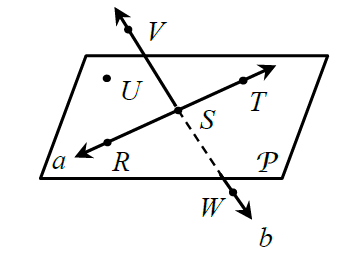
S or W
100
Given a line segment TR with endpoints T(-1,3) and R( 7,-1). Find the midpoint of TR?
(3,1)
100
Given two parallel lines cut by a transversal, which 3 angle pairs are congruent?
corresponding, alternate interior and alternate exterior
100
Solve for x.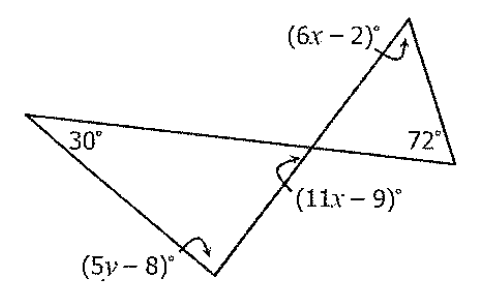
x=7
100
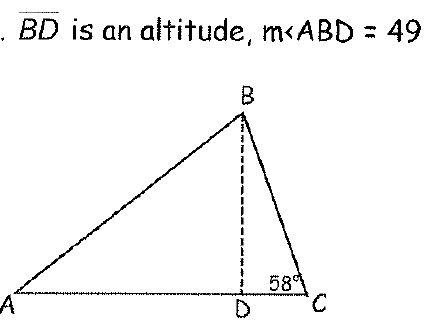
Find m<A
41
200
Give another name for plane P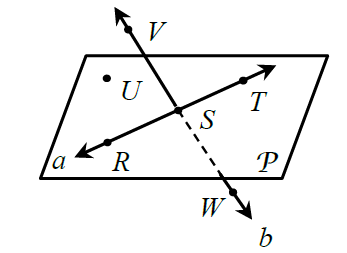
Plane URS or UST (3 non-collinear points)
200
Find the length of GH if G is (2,8) and H is (-3,1)
square root 74
200
Given two parallel lines are cut by a transversal, which 2 angle pairs are supplementary?
same side interior, same side exterior
200
Solve for x.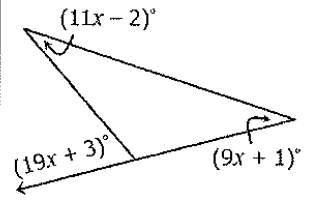 
x=9
200
Find DE.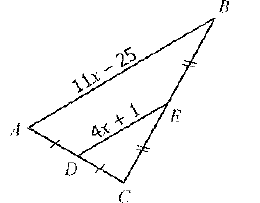
DE=37
300
The intersection of line b and plane P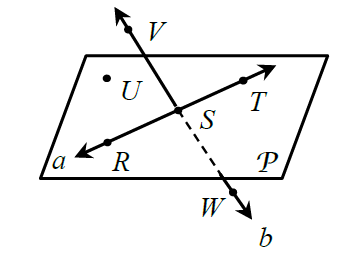
Point S
300
If A is (2, -3) and it is translated with the following rule (x-6, y+8), what are the coordinates of A'?
(-4, 5)
300
Solve for x.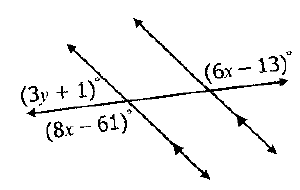 
24
300
Which congruency theorem proves triangle CEF is congruent to triangle DEF?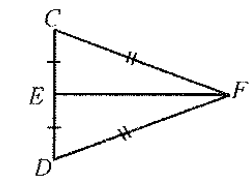
side-side-side
300
Find TA/
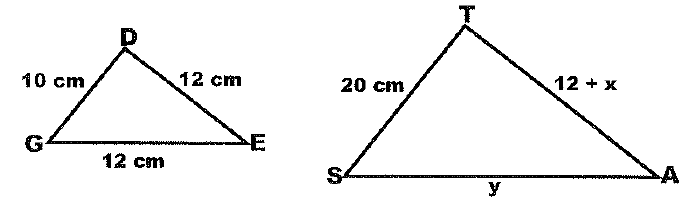
24
400
Give a counter-example for the following statement: All composite numbers are greater than 5.
4 is less than 5 and is a composite number
400
Write an equation parallel to y=5/2x+3, through the following point (4,9).
y=5/2x-1
400
Solve for x.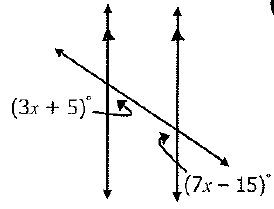
x=19
400
Which congruency theorem proves triangle DAJ is congruent to triangle EAM?
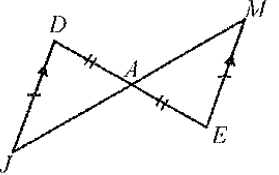
Angle-side-angle or side-angle-side
400
What theorem proves the triangles are similar.
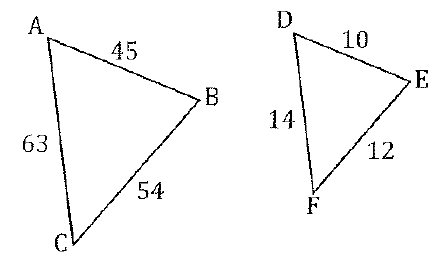
SSS
500
What is the contra-positive of this statement: If two angles are complementary then they are each 45 degrees.
If two angles are not each 45 degrees then they are not complementary.
500
Write an equation that is perpendicular to y=-3/2x-1, that goes through the point (8, -5)
y=-3/2x+7
500
If angles 3 and 5 are congruent then which theorem proves line p is parallel to q?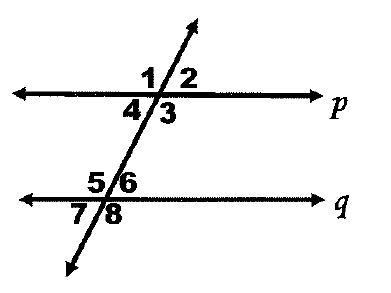
alternate interior angles converse
500
Name 5 theorems that prove triangles are congruent.
SSS, SAS, AAS, ASA, HL
500
Solve for x.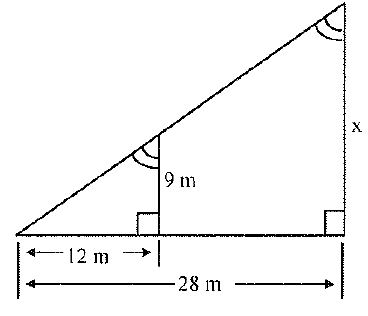
x=21