Algebra Proofs
Segment Proofs
Angle Proofs
Definitions
100
The first reason on any algebra proof is this ____.
Given
100
Point a is in between point C and point B. Point C and point B are collinear. Therefore CA + AB = AC. This is an example of which postulate?
Segment Addition
100
The following is an example of the ______ property.
m<1 = 150 degrees.
m<1 + m<2 = 180 degrees
150 + m<2 = 180 degrees
substitution?
100
Supplementary Angles add to _______°
180°
200
Give an example of the subtraction property.
x + 8 = 58
x = 50
200
Give an example of the segment addition postulate, with a drawing. (Use the points A, B, and C).
AB + BC = AC
200
Explain how the angle bisector theorem is different then the angle addition postulate.
With the angle bisector theorem the angle is split into two equal pieces.
200
The point that divides a segment into two congruent segments.
Midpoint
300
This would be an example of the which property?
If /_A+/_B=180° and /_B+/_C=180°
then
/_A=/_C
Transitive
300
True/False. Definition of congruence is only used with segment proofs.
False.
300
Give an example of a property that is used just with angles.
Angle Addition Postulate
Angle Bisector
Supplementary Angles
Complementary Angles
300
A pair of opposite angles made by two intersecting lines that are congruent.
Vertical angles
400
What is the last reason for the following algebra proof?
What is the division property of equality?
400
This reason justifies statement 2 in the following proof.
Definition of midpoint
400
Which theorem tells us that
If
/_1 and /_2 are supplements
and /_2 and /_3
are supplements.
Then
/_1 cong/_3
Congruent supplements theorem
400
Two angles that are next to one another, have a common side, a common vertex, and don't overlap.
Adjacent Angles
500
What is a logical 2nd statement (assuming the first is a given):
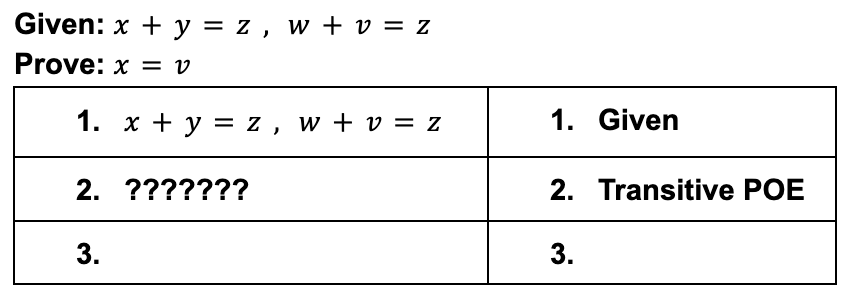
x + y = w + v
500
What would be the last reason in the following proof?
Definition of segment congruence
500
Give statement #6
m<1 + m<5 = 180
500
A statement that needs to be proven before we can use it.
We prove these with definitions, postulates, and properties.
Theorems