Interior Angle Sum
Exterior Angle Sum
Using Interior and Exterior Angles
Quadrilaterals
The Parallelogram
Rhombus Proofs
100
Name all interior angles labelled in the shape below
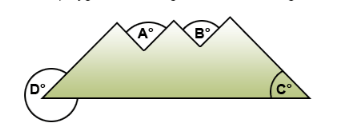
C
100
Which angle is the exterior angle?
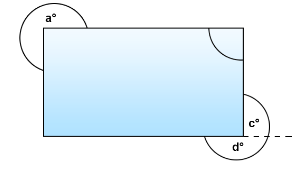
c
100
What is a+b?
180 degrees
100
Which term most accurately describes the quadrilateral that has opposite parallel sides but no right angles.
Parallelogram
100
Name 3 properties of parallelograms
Opposite sides are parallel. Opposite sides are congruent. Opposite angles are congruent. Adjacent angles are supplementary
100
What is the measure of angle a1?
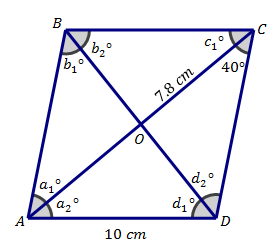
40 degrees by Alt Interior Angles
200
What is the formula for the sum of the interior angles of a polygon?
180(n-2)
200
What is the sum of the exterior angles of a convex polygon?
360 degrees
200
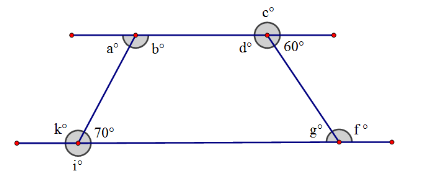
b = 110 degrees, what is the measure of angle g?
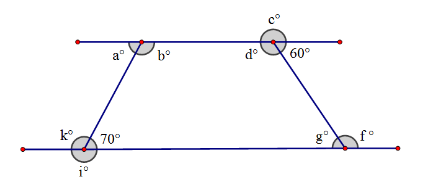
60 degrees by alternate interior angles
(Note: g=110 tells us that our top and bottom sides are parallel, which allows us to use transversal properties)
200
Name 3 special types of parallelograms
rectangles, rhombi, squares
200
What is the relationship between angles a and b?
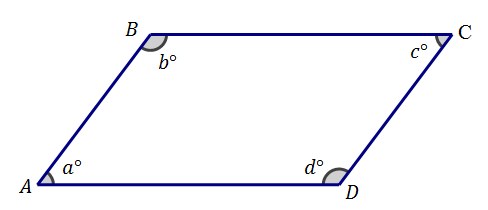
They add to 180 degrees
200
What is the length of diagonal AC?
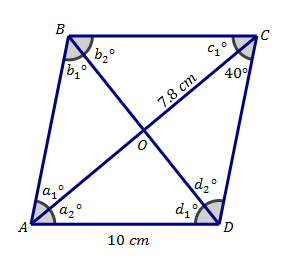
7.8*2 = 15.6
300
What is the sum of the interior angles of the shape shown below?
180(n-2) = 180(5-2) = 180(3) = 540
300
Solve for x
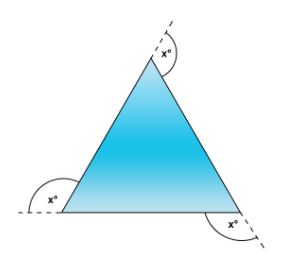
x = 360 divide 3 = 120
300
What is the sum of k+i?
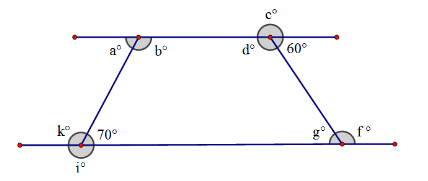
360-70 = 290 degrees
300
What is the defining characteristic of a kite?
they have 2 pairs of consecutive congruent sides
300
Parallelogram ABCD is a square. The length of side BC = x + 4 and the perimeter of ABCD = 80. What is the length of side BC?
perimiter = 4(x+4) = 4x+16 = 80
4x = 64, x=16.
BC = x+4 = 16+4 = 20
300
What is the measure of angle L
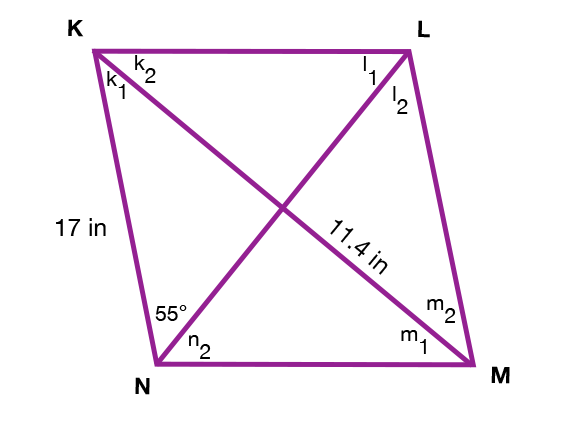
55*2 = 110
400
What is the sum of the interior angle of a shape with 20 sides?
180(20-2) = 180(18) = 3240
400
Find the measure of angle r
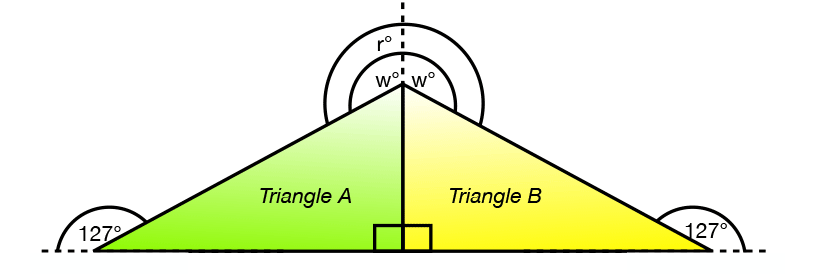
w = 360-90-127 = 143
r = 2w = 286
400
What is the measure of angle y?
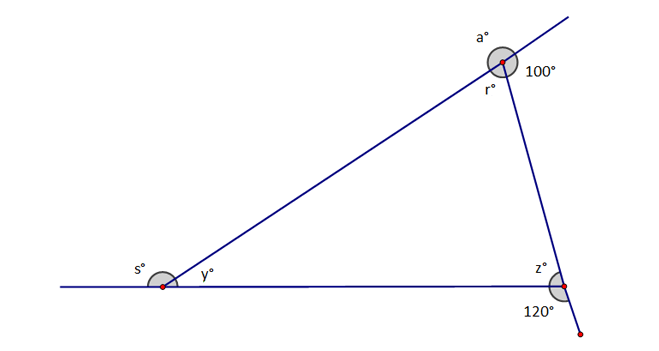
40 degrees
400
Find the measure of angle B
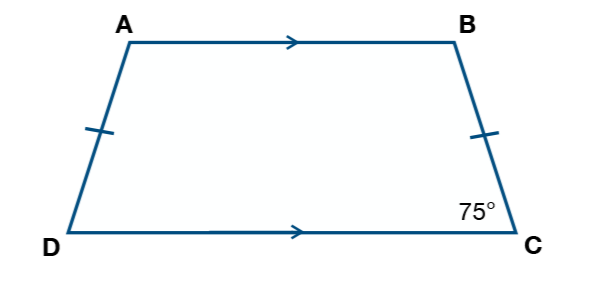
180-75 = 105 degrees
400
Find the area of the rectangle below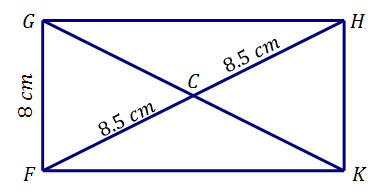
First we find the width using the Pythagorean theorem.
x^2+8^2=17^2
x^2+64 =289
x^2 = 225
x = 15
We now use the length and width to find the area of the rectangle: A = l*w = 15*8 = 120
500
What is the sum of the interior angles of a decagon?
180(n-2) = 180(10-2) = 180(8) = 1440
500
Prove that the exterior angles of a quadrilateral sum to 180 degrees.
Take a random quadrilateral ABCD.
All 4 angles of ABCD are made of up a pair of interior and exterior angles that are supplementary.
Let us label the interior angles as a,b,c,d and the exterior angles a',b',c', and d'.
We know that (a+a') = (b+b') = (c+c') = (d+d') = 180. It follows that (a+a')+(b+b')+(c+c')+(d+d') = 4*180 = 720
We can rewrite this sum as a+b+c+d+a'+b'+c'+d'=720
We know that the interior angles of a quadrilateral sum to 360 degrees, so we can substitute 360 in for a+b+c+d, which gives us:
360 + a'+b'+c'+d' = 720
a'+b'+c'+d' = 360.
Since a',b',c',and d' are our exterior angles, and they all add to 360 degrees, our proof is complete.
500
What is the measure of angle s?
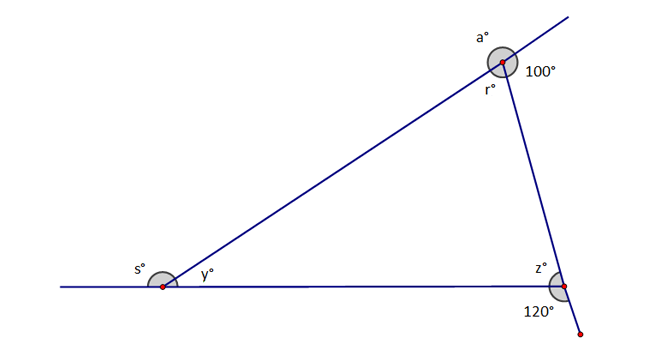
140 degrees
500
If AD = 3x + 18, AB = 5x + 10, and BC = 12x + 2, what is BC?
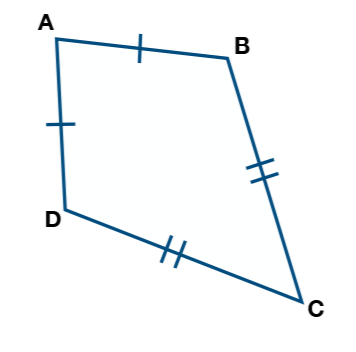
AB = AD, 3x+18 = 5x+10
2x = 8
x=4
BC = 12x+2 = 12(4)+2 = 50
500
Prove that opposite sides of a parallelogram are congruent.
consider an arbitrary parallelogram.
We know that opposite sides are equal by definition.
We can draw a diagonal that is congruent to itself by the reflexive property.
This gives us two triangles that are congruent by SSS.
This gives us two opposite angles that are congruent by CPCTC