Show that these two ratios are in proportion.
(50) / (100)= (1) / (2)
- Cross Multiply. Cross products = 100
- 50 is half of 100
- other
Similar polygons have the same ___ but different ___.
Same Shape & Different Size
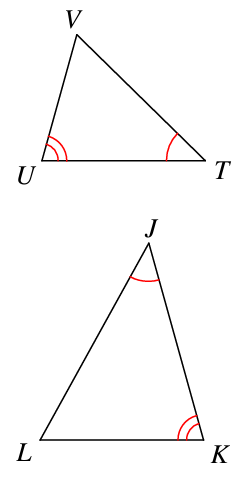
How can you prove these triangles similar?
AA~
What is a ratio?
A comparison of 2 quantities.
Dilations are transformations that create ______ images.
Similar
How many subway stations are there in Cambridge?

5
Alewife, Porter, Harvard, Central, & Kendall
Are these two ratios in proportion? Prove it.
(13) / (17) = (78) / (102)
Yes
(13)(102) = (17)(78)
1,326 = 1,326
Cross-products are equal.
This shape is universally similar to all others of its kind and the ratio of its circumference to diameter is always approximately 3.14.
What is a circle?
How can you prove these triangles similar?
SSS~
Find the length of the missing side.
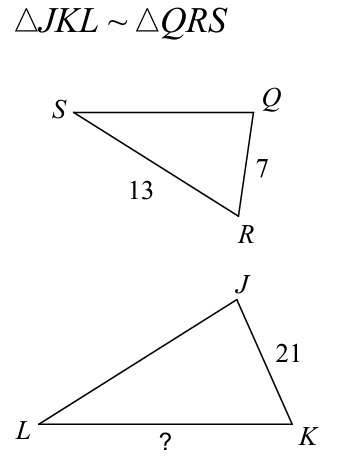
x = 39
Identify the pre-image.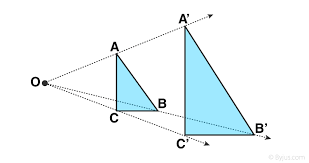
triangleABC
Who does this logo belong to?

Harvard University
Solve for x.
2/5 = x/75
x = 30
This polygon has 4 right angles and is universally similar to all others of its kind.
What is a square?
How can you prove these triangles similar?
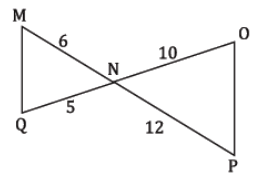
SAS~
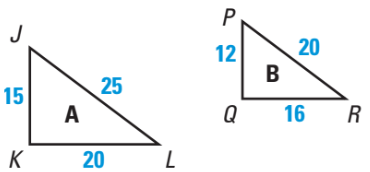
Find the missing side length.
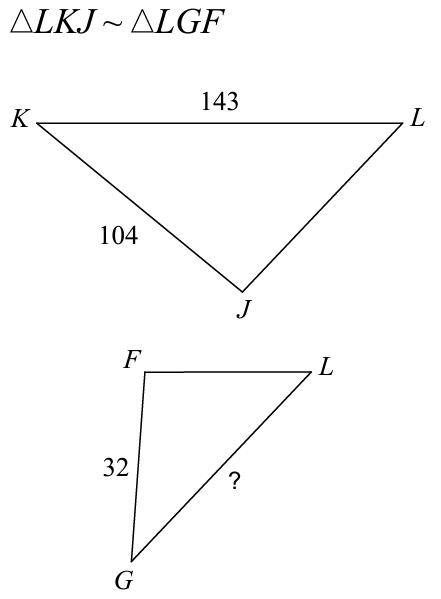
x = 44
What happened to the pre-image?
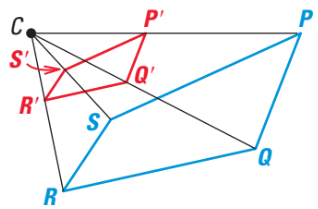
It shrunk.
Where in Cambridge is this?

Fresh Pond
Solve for x.
4/13 = 16/x
x = 52
Corresponding ___ in similar polygons are always congruent.
Angles
Are these triangles similar? If so, which theorem (AA~, SSS~, or SAS~) would prove it?
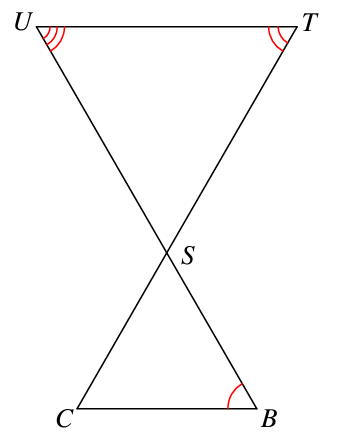
Not enough information
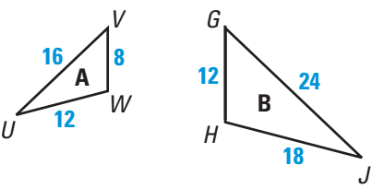
What is the scale factor?
triangleA ~ triangleB
3/2 (1.5)
2/3 (0.66666)
This is the value of m in this dilation.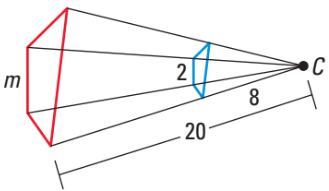
What is 5?
What is the official name of this bridge?

+200 BONUS: What is this bridge's nickname?
OFFICIAL NAME: Longfellow Bridge
+200 BONUS: Salt and Pepper Bridge
Solve for x.
9/x = x/25
x = 15
What is the ratio of similarity?
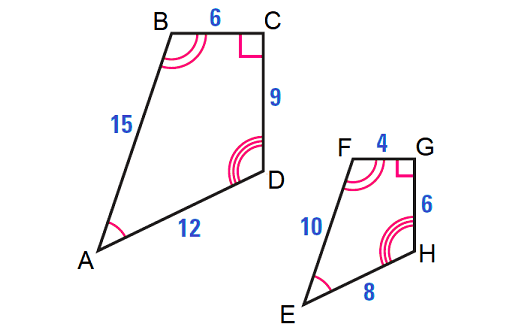
3/2
Are these triangles similar? If so, explain how you know and complete the similarity statement.
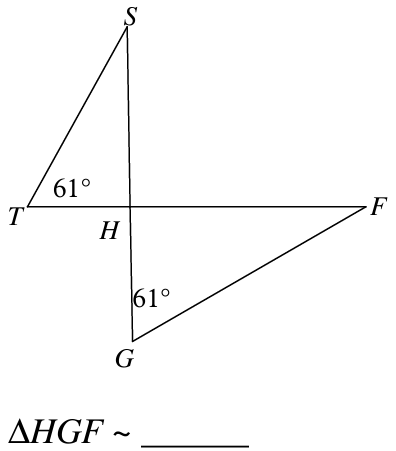
Yes, because of AA~.
triangleHTS
Are these triangles similar? Prove it.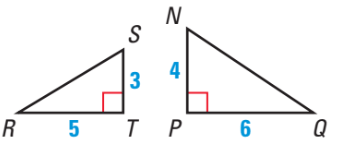
No. There is no ratio of similarity.
3/4 = 0.75
5/6 = 0.83333
What is the scale factor of this dilation?
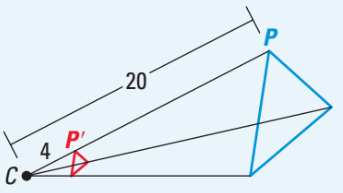
1/5
Where in Cambridge is this?
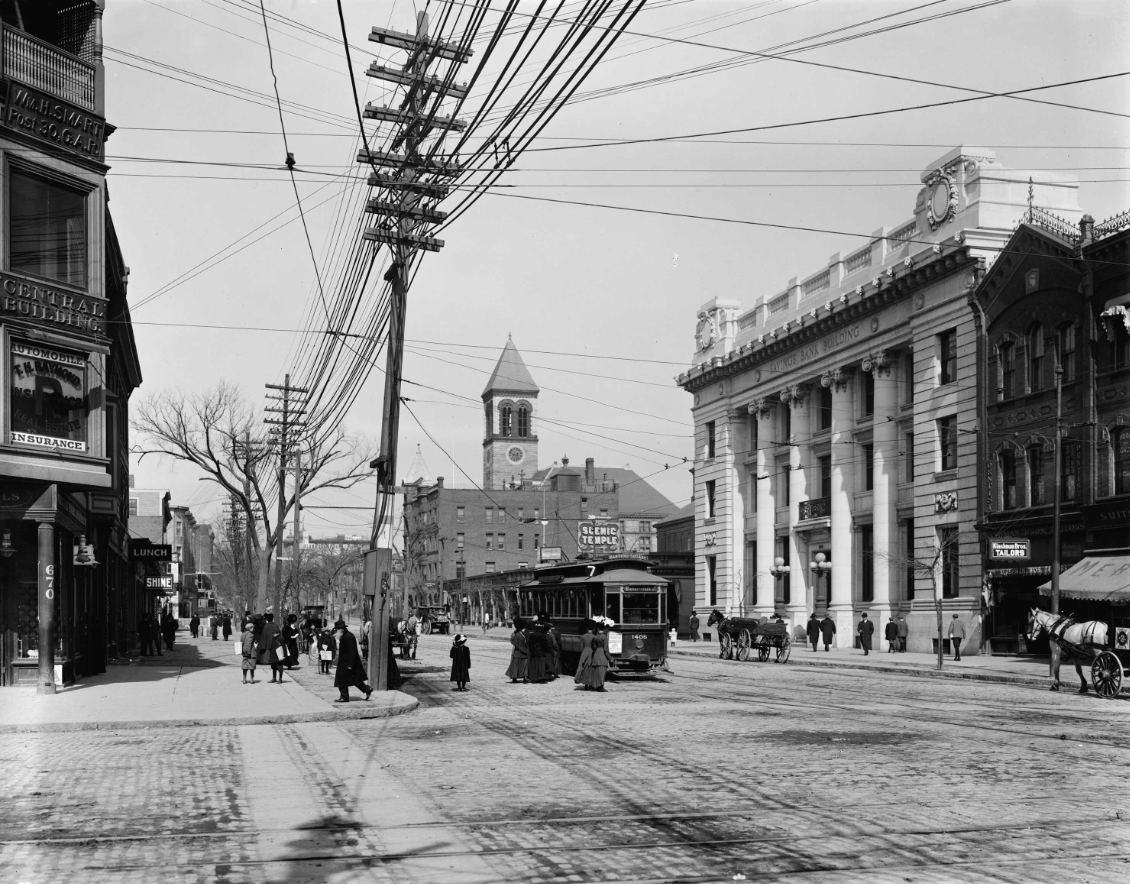
+250 BONUS: What street are we looking at?
Central Square (circa 1900)
Mass Ave (Corner of Mass Ave & Western Ave)