What does it mean?
Mind your p's and q's
Let's make a statement
Follow the Law
(Blank)
100
An example that opposes or contradicts a statement
What is a counterexample?
100
A "p" represents this part of a conditional statement
What is the hypothesis?
100
State the hypothesis of the following:
"If today is Friday, then tomorrow is Saturday."
What is "today is Friday"?
100
Finish the logic statements using the law of syllogism:
1) If it rains, then the game will be cancelled.
2) If the game is canceled, then I will go to the mall.
3) ?
What is "If it rains, then I will go to the mall"?
100
Symbolically, we write this phrase as
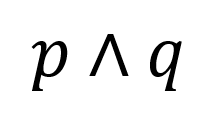
What is " p and q"
200
An if-then statement
What is a conditional statement?
200
A "q" represents this part of a conditional statement
What is the conclusion?
200
State the negation of the following :
"I am cold."
What is "I am not cold"?
200
Finish the logic statements using the law of detachment:
1) If it rains, then the game will be cancelled.
2) It rains.
3) ?
What is "The game is cancelled"?
200
When a conclusion is arrived at through the use of the Laws of Logic, it is _____________ even if it is not true.
What is valid?
300
An if-and-only if statement
What is a biconditional statement?
300
Given p implies q, this related conditional is written as
q --> p
What is the converse?
300
Make a conditional statement from the following statement:
"All whole numbers are integers."
What is "If a number is a whole number, it is an integer"?
300
Finish the following logic statement using the law of contraposition:
1) If we go trick or treating, then we will get candy.
2) We will not get candy.
3)?
What is "We did not go trick or treating"?
300
Valid or not valid? Explain.
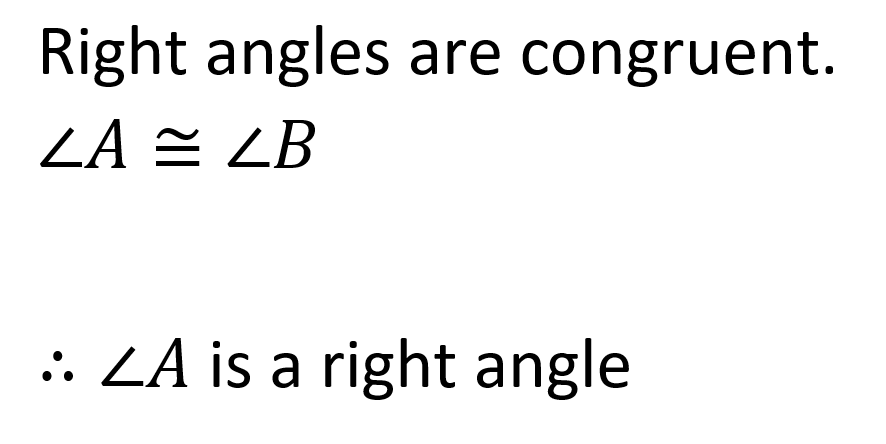
What is "not valid?"
Converses are not always true.
400
A statement that results from switching the hypothesis and the conclusion
What is the converse?
400
Given p implies q, this related conditional is written as
~p -> ~q
What is the inverse?
400
State the converse:
"If Melissa came to class every day, then she passed the class."
What is "If Melissa passed the class, then she came to class every day"?
400
Finish the following logic statement using the law of syllogism:
1) If you are in Miss Frizzle's class, then she is your favorite teacher.
2) If Miss Frizzle is you favorite teacher, you will get candy.
3) ?
What is "If you are in Miss Frizzle's class, then you will get candy."
400
The symbolic form of the following argument:
What is:
p: you are a man
q: you are mortal
p ->q
p
therefore q
500
A statement that results from switching and negating the hypothesis and conclusion
What is a contrapositive statement?
500
p iff q
is an example of this type of statement.
What is a bi-conditional statement?
500
Given the contrapositive statement: "If Carl does not go to Geometry every day, then he is not passing the class"
What is the original conditional statement?
What is "If Carl is passing the class, then he is going to Geometry every day"?
500
Finish the logic statement using the law of detachment:
1) If you do your homework, you will get a 100.
2) You do your homework.
3) ?
What is "You get a 100"?
500
The valid conclusion to the following argument:
This cake is either red velvet or chocolate.
It's not chocolate cake.
What is "the cake is red velvet."