A translation is when you move a shape WITHOUT _____________
Rotating or reflecting it
A reflection is when you do what to a figure?
Flip it or make a mirror image of it.
A rotation is when you do what to a figure?
Turn or Spin
A combination between a reflection and translation.
Glide Reflection
What are three types of transformations?
Translation, rotation, reflection, or dilation.
Find the new coordinates of (10,12) if you translate the point three units left and 4 units up.
(7,16)
Find the new coordinates of (3,-2) after you reflect the point over the y-axis.
(-3,-2)
After you rotate the point (5,4) 90º counterclockwise about the origin, what what are the coordinates of the image?
(-4,5)
Find the new coordinates of (3,-2) if you translate using the rule (x+2, y-3) and then reflect over the x-axis.
(5,5)
After a translation reflection, or rotation, the preimage and the image should always be _____
Congruent
Write a vector or a rule for moving a shape 3 units to the left and 7 units up.
〈–3, 7〉or (x–3,y+7)
Write the coordinates of A(5, –4) after a reflection in the line y = x
A'(–4, 5)
Name the rotation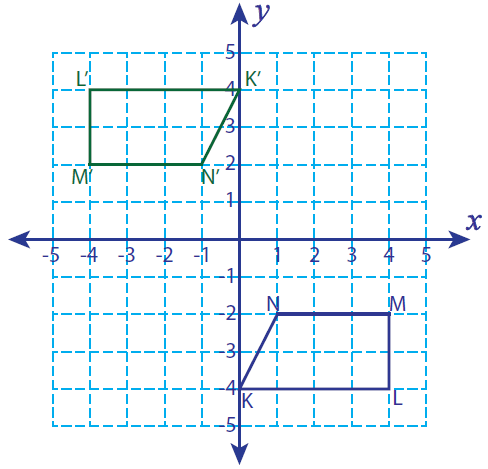
180 Degrees
What is the result if A(9,4) is reflected over y=x and then rotated 180 degrees.
(-4,-9)
What is the type of transformation that produces congruent figures.
Rigid transformation (Isometry)
What is the PRE-IMAGE of the point H'(9,3) if it was translated using the rule (x+2, y-5)?
H(7,8)
Write the coordinates of A(5, –4) after a reflection in the line y = –x
A'(4, –5)
What is the same as 90 clockwise?
270 CCW
What is the result of point Q(4,5) when it is reflected over y=-x and then rotated 90 degrees counterclockwise.
(4,-5)
What property is changed under a dilation?
Size
Write the coordinates of ∆LMN after a translation on the vector 〈6, –2〉
L(0,3) M(–2,–4) N(1,–9)
L'(6,-1), M'(4, –6), N'(7, –11)
Write the coordinates of DEFG after a reflection over the line y=–x. D(6,5) E(–5,8) F(8,7) G(–8,5)
D'(-5,-6), E'(-8,5), F'(-7,-8), G'(-5,8)
Write the coordinates of ∆JKL after a rotation of 90º CCW about the origin. J(5,6) K(7,9) L (1,2)
J(-6,5), L(-9,7), L(-2,1)
What is point D (-6,2) after being reflected over x=1 and then translated down 3.
(8,-1)
What property never changes under dilation, rotation, reflection, or translation?
Angles