Translations
Reflections
Rotations
Dilations
Mapping a Figure Onto Itself
100
Point A has coordinates (4,6). What are the coordinates of A' after a translation with rule (x,y) -> (x-2, y+1)?
A' (2,7)
100
If E has coordinates (3,2), what is the image of E after a reflection of the y-axis?
E (-3,2)
100
If J has coordinates J(8,2), what are the coordinates of its image after a rotation of 180 degrees clockwise around the origin?
J'(-8,-2)
100
If point N has coordinates (-4,5), what are the coordinates of the image after a dilation with scale factor 3 centered at the origin?
N' (-12, 15)
100
If a regular octagon is rotated around its center, what is the minimum number of degrees it takes to carry the octagon onto itself?
45 degrees
200
Point B has coordinates (-3,7). What are the coordinates of B' after a translation that moves B 4 units to the right and 5 units up?
B' (1,12)
200
If point F has coordinates F (3, 10), what are the coordinates of F' after reflecting over the line x=3?
F'(3,10)
200
Point K has coordinates (-3,4). What are the coordinates of K' after a rotation around the origin going counterclockwise 90 degree?
K'(-4,-3)
200
Point P has coordinates (1,-3). What are the coordinates of P' after a horizontal stretch (with respect to x=0) with scale factor 9?
P'(9,-3)
200
Draw a square and all of the lines of symmetry on it (lines that would make the shape map onto itself after a reflection)
300
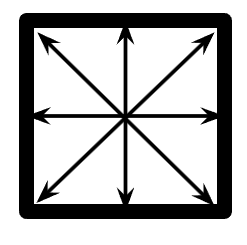
A translation, reflection, and rotation all _______ __________. (Hint, a dilation is not one of these)
Rigid Motion
300
If G has coordinates (-5,5) and gets reflected over the x-axis, what are the coordinates of the image?
G' (-5, -5)
300
L( -7,1) is being rotated around the origin 90 degrees clockwise. What are the coordinates of L'?
L'(1,7)
300
What is the scale factor of the following points if they are dilated around the origin?
Q(-24,32) -> Q'(-6, 8)
k=1/4
300
What is the minimum number of degrees that a regular decagon must rotate about its center to carry it onto itself?
36
400
If C has coordinates (6,-2) and C' has coordinates (0,-1), what is the rule that maps C onto C'?
(x,y) -> (x-6, y+1) or left 6 units and up 1 unit
400
If points H and H' have the coordinates H (-7,3) and H'(-3,7), what line did H reflect over to map onto H'?
y = - x
400
Point M has coordinates (2,1). If you rotate M 90 degrees counterclockwise, then rotate it 180 degrees clockwise, what are the coordinates of your image going to be?
M'' (1,-2)
400
A point has that has coordinates (-7,4) is being dilated by a vertical stretch (with respect to y=0) by a scale factor of 1/2. What are the coordinates of the image?
(-7,2)
400
Name a regular polygon that would carry onto itself after a rotation of 300 degrees about its center.
Hexagon or Nonagon (dodecagon would work too for a 12 sided shape)
500
If the translation rule is (x,y) -> (x+3, y-10) and D' has coordinates (6, 7), what are the coordinates of D?
D (3, 17)
500
What are the rules for reflecting over the x-axis, y-axis, line y=x, and line y= - x
X-axis: (x,y) -> (x,-y)
Y-axis: (x,y) -> (-x,y)
y=x: (x,y) -> (y,x)
y= -x: (x,y) -> (-y,-x)
500
What are the rules for rotating around the origin 90 degree counterclockwise, 180 degrees counterclockwise, and 270 degrees counterclockwise?
90: (x,y) -> (-y,x)
180: (x,y) -> (-x,-y)
270: (x,y) -> (y,-x)
500
The equation of a line is 3y=5x-15. What is the equation of the image of this line after a dilation of 4 around the origin?
y=5/3x-20
500
Name each polygon with the following number of sides. 5, 7, 9, 10
Pentagon, Heptagon (Septagon), Nonagon, and Decagon