A point starts at (3,5). You translate it left six and up 2. What quadrant is the image in?
Quadrant II
You reflect a figure that is completely in quadrant III over the y-axis. What quadrant is the image in?
Quadrant IV
The point (-4,-5) is rotated 270° clockwise. What quadrant is the image in?
Quadrant IV
Quadrant II
 Does the figure have line symmetry, rotational symmetry or both?
Does the figure have line symmetry, rotational symmetry or both?
Line symmetry only
Find the new coordinates of (10,12) if you translate the point three units left and 4 units up.
What is (7,16)?
Find the new coordinates of (3,-2) after you reflect the point over the y-axis.
What is (-3,-2)?
Find the new coordinates of (5,4) after you rotate the point with 180º.
What is (-5, -4)?
Find the new coordinates of (3,-2) if you dilate the point with a scale factor of -4.
What is (-12,8)?
Name the order and degree of rotational symmetry. 
Order = 4; Degree = 90°
Write the rule for point (x,y) after it moves 3 spots to the left and 7 spots up.
translate along <-3, 7>
or
(x,y)→(x-3,y+7)
Write the rule for point (x,y) after it is reflected over the y-axis.
What is (x,y)→(-x,y)?
Write the rule for point (x,y) after it rotates 90º?
What is (x,y)→(-y,x)?
Write the rule for point (x,y) after it is dilated with a scale factor of 6.
What is (x,y)→(6x,6y)?
How many lines of symmetry for the following image? 
4: Horizontal, Vertical, Diagonally with a positive slope, Diagonally with a negative slope
Write the name of the line and rule for the following translation:
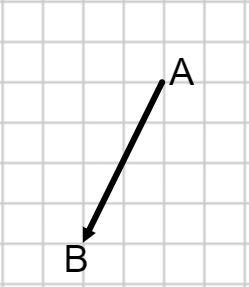

<-2,-4>
A picture with one point (-3,4) was reflected over the x axis. What should be the new coordinates of the point?
What is (-3,-4)?
Figure QRST has vertices Q(2,-1), R (6,-1), S(6,-3) and T(2,-3). Which will be the coordinates of vertex R after the rectangle is rotated 90º counterclockwise about the origin?
What is (1,6)?
Triangle BCD was dilated around the origin by a scale factor of 2. The coordinates of the new triangle are B' (4,4) C' (4,0) and D' (6,2). What are the coordinates of the of the original triangle?
What is B(2,2) C(2,0) and D(3,1)?
 Which of the three kinds of symmetry does this figure have?
Which of the three kinds of symmetry does this figure have?
Line and rotational
write the new coordinates for each point ∆LMN after a translation of 6 units to the right and 4 units down. L(0,3) M(6,4) N(3,9)
What is L'(6,-1), M'(12,0), N'(9,5)?
write the new coordinates of DEFG after a reflection over the x-axis. D(5,5) E(5,8) F(8,8) G(8,5)
What is D'(5,-5), E'(5,-8), F'(8,-8), G'(8,-5)?
Name the new coordinates for ∆JKL after a rotation of 180º about the origin. J(5,6) K(7,9) L (1,2)
What is J(-5,-6), L(-7,-9), L(-1,-2)?
The new coordinates for ∆DEF after a dilation with a scale factor of 1/2. D(2,8) E(2,2) F(6,2)
What is D'(1,4), E'(1,1), F'(3,1)?
Define line, point, and rotational symmetry
A figure has line symmetry is it can be mapped onto itself by a reflection over a line
A figure has point symmetry if it can be mapped onto itself by rotating 180 degrees about the center point
A figure has rotational symmetry if it can be mapped onto itself by rotating less than 360 degrees.