Here are 4 common congruence statements:
Definition of Midpoints
Reflexive Property
Definition of Bisector
Vertical Angle Theorem
Which two can you simply assume? Which two do you have to be told specifically?
Reflexive Property
Vertical Angle Theorem
Must be told:
Definition of Midpoint
Definition of Bisector
Solve for x

2(10)=2x-6
10=x-3
13=x
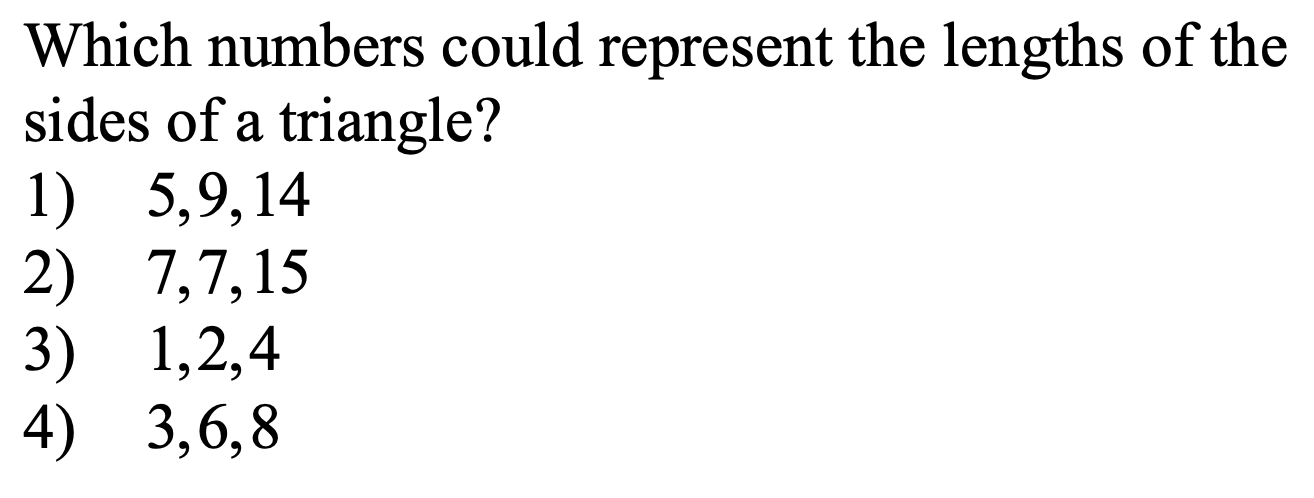
4) 3+6=9
9>8
Name the sides of the triangle from shortest to longest.
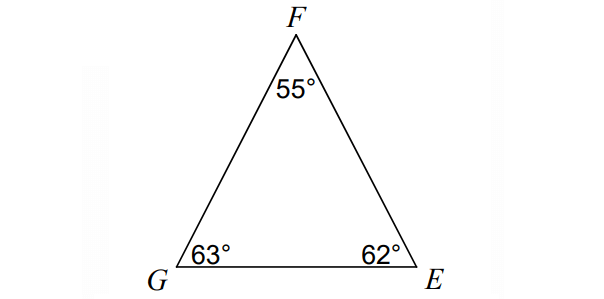
\bar(GE),\bar(GF),\bar(FE),
Determine if the triangles are congruent. If YES, state the reason. If not, write NO
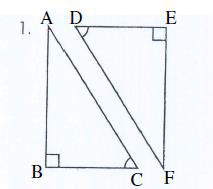
No!
Not HL because we only know the two angles are congruent. Nothing about the sides.
Solve for x and
DF

3x+1=2(x+3)
3x+1=2x+6
x=5
DF=2(9)=18
Two sides of a triangle are 7 and 11. Which of the following represent the possible lengths of the third side?
a)
x>=4
b)
x<=18
c)
4<x<18
d)
7/11<x<11/7
c)
Name the lengths of the sides from shortest to longest.
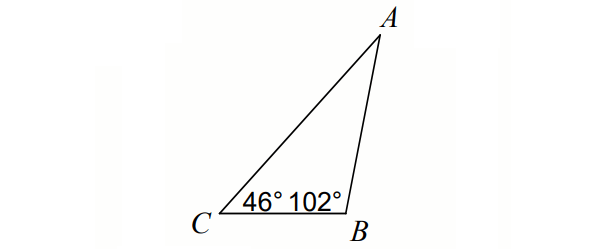
m\angleA=32
\bar(CB),\bar(AB),\bar(CA)
Determine if the triangles are congruent. If YES, state the reason. If not, write NO
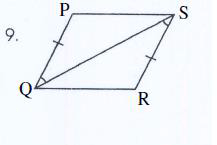
Yes! SAS because of the reflexive property.
Solve for y and z
4y-9=3y+4
y=13
2(6z-1)=7z+8.5
12z-2=7z+8.5
5z=10.5
z=2.1
The lengths of two sides of a triangle are 12 and 19. Create an inequality that represents the range of possible lengths for the third side of the triangle.
7<x<31
\DeltaBOY~=\DeltaGRL
Solve for x and y
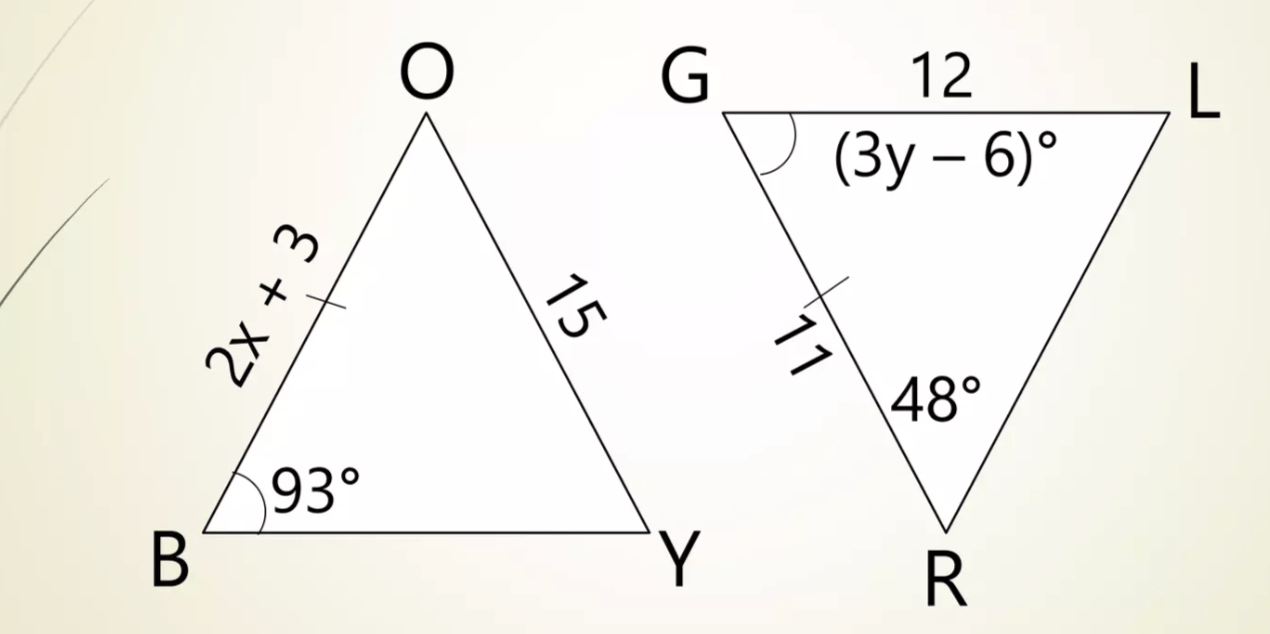
\angleG~=\angleB
3y-6=93
y=33
\bar(BO)~=\bar(GR)
2x+3=11
x=4