Theorems
Proofs
Solve for x
Additional Info
Surprise!!
100
By what method can you prove these two triangles are congruent (if any)?
Not
100
What is the reason we can mark this as true:
∠BCA ≅ ∠ECD
Vertical angles
100
Given that triangle ABC is congruent to triangle DEF, find the measure of angle F.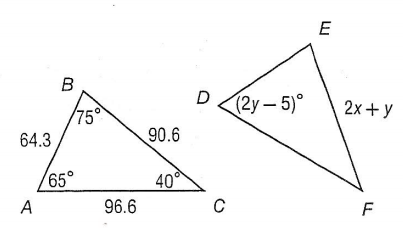
40
100
What congruent parts information would we need to know for the triangles to be congruent by ASA?
CE=CD
100
What piece of information can you deduce from this picture and why?
AB is congruent to AB by the reflexive property
200
By what method can you prove these two triangles are congruent (if any)?
None
200
Given: C is the midpoint of AE.
As a result of the given statement, what can you deduce about the triangles?
AC is congruent to CE
200
Find the measure of angle F.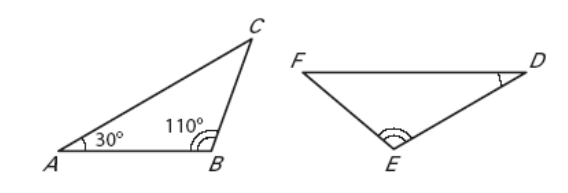
40
200
The additional information needed to prove the two triangles are congruent using HL theorem
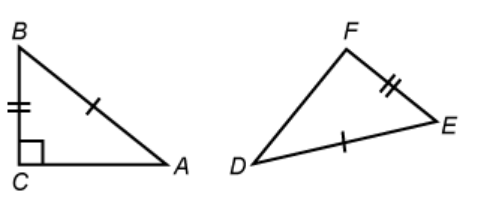
angle F is 90 degrees
200
List all the ways that you can prove triangles congruent. List the two ways you can NEVER prove triangles are congruent.
ASA, SSS, SAS, AAS, HL
No butts no batteries
300
By what method can you prove these two triangles are congruent (if any)?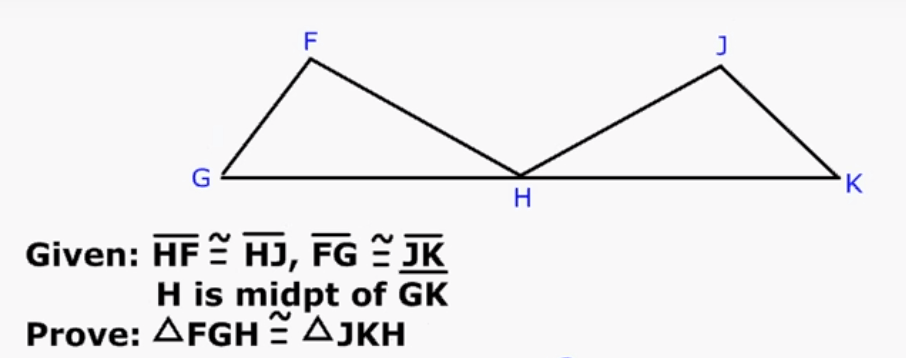
SSS
300
Given: AE bisects BD
Name the parts we are allowed to mark congruent:
BC=CD
300
These two triangles are congruent, find the value of x.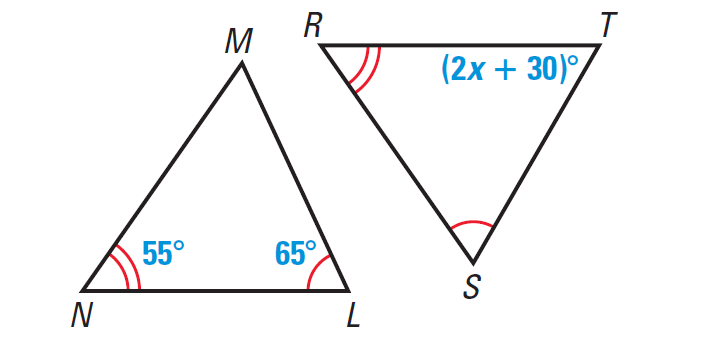 
x=15
300
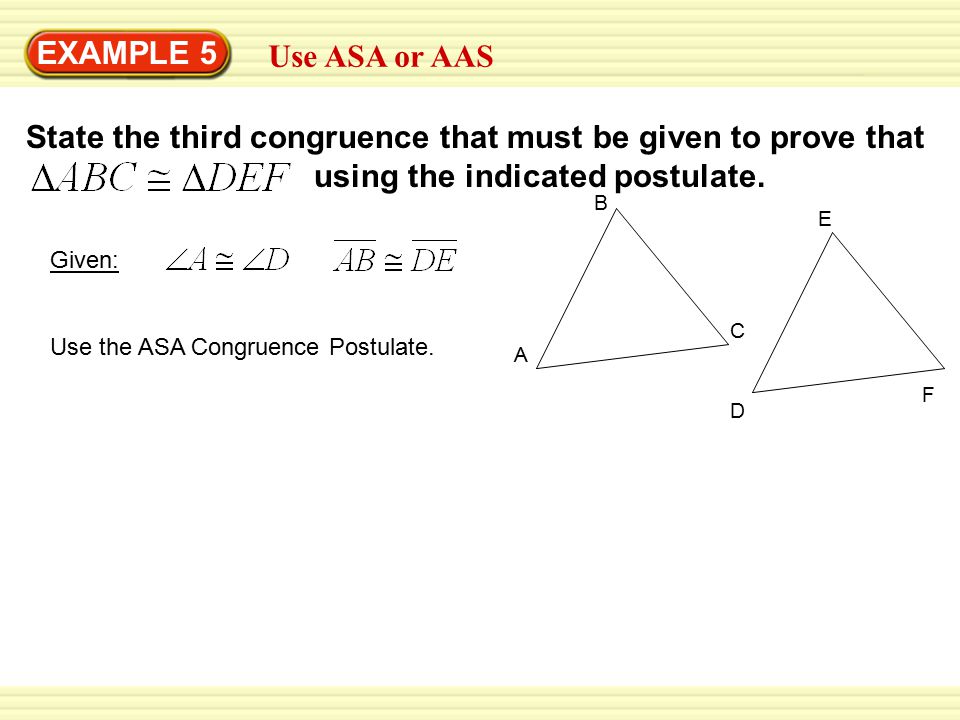
angle B equals angle E
300
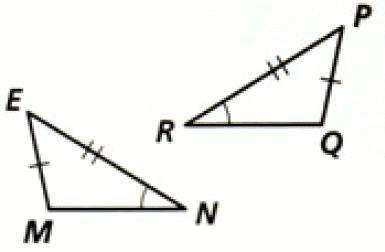
Name 3 ways these two triangles can be congruent and how you got those three ways.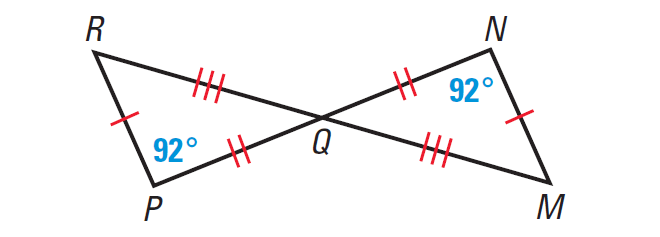 
SSS
SAS
ASA
AAS
400
If we know segment KA bisects angle K, are triangles JAK and NAK congruent? How?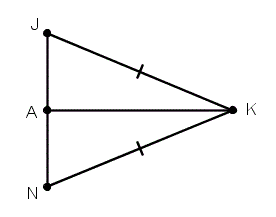 
Yes, by SAS
400
Given:
BD bisects ∠ABC
What can you deduce from the given information?
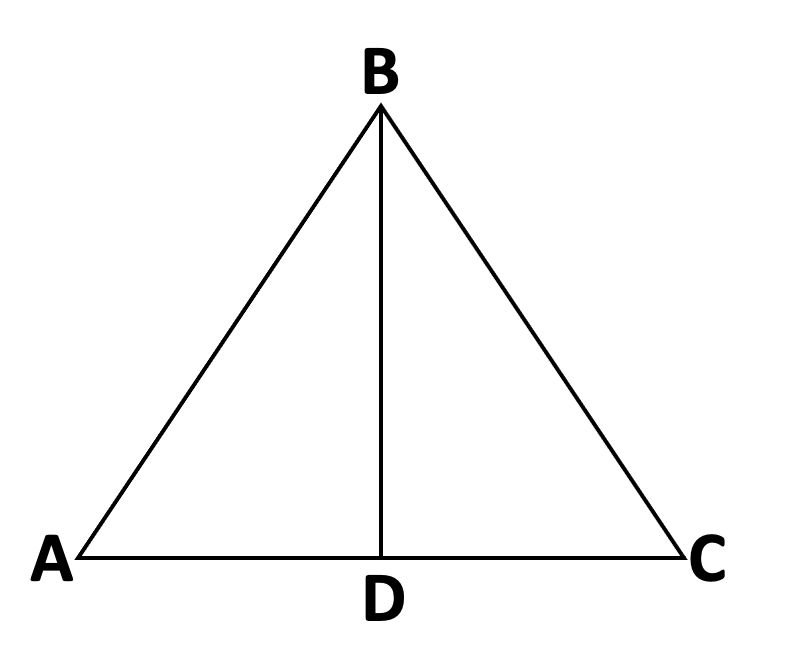
angle ABD is congruent to angle DBC
400
If these two triangles are congruent, what is the value of x?
x=3
400
What congruent parts would make these triangles congruent by AAS?
Either BC=EF
or AC=DE
400
Congruence statement for the triangles represented by:
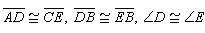
What is
△ADB≅△CEB
500
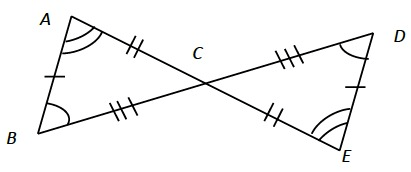
Are these triangles congruent? Name all the theorems you could have used.
SSS
SAS
ASA
AAS
500
Assume:
A is the midpoint of ED and BC.
What three statements prove the triangle congruent, and what theorem proves the triangles congruent?
AE=AD
BA=AC
Angle CAE is congruent to angle DAB
500
Solve for x? (Hint* angles across from congruent sides are congruent*)
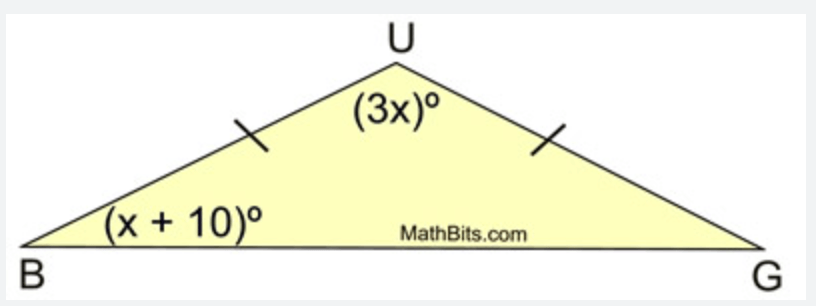
x=32
500
Given AC bisects ∠BAD, what else is needed to prove the triangles are congruent through AAS
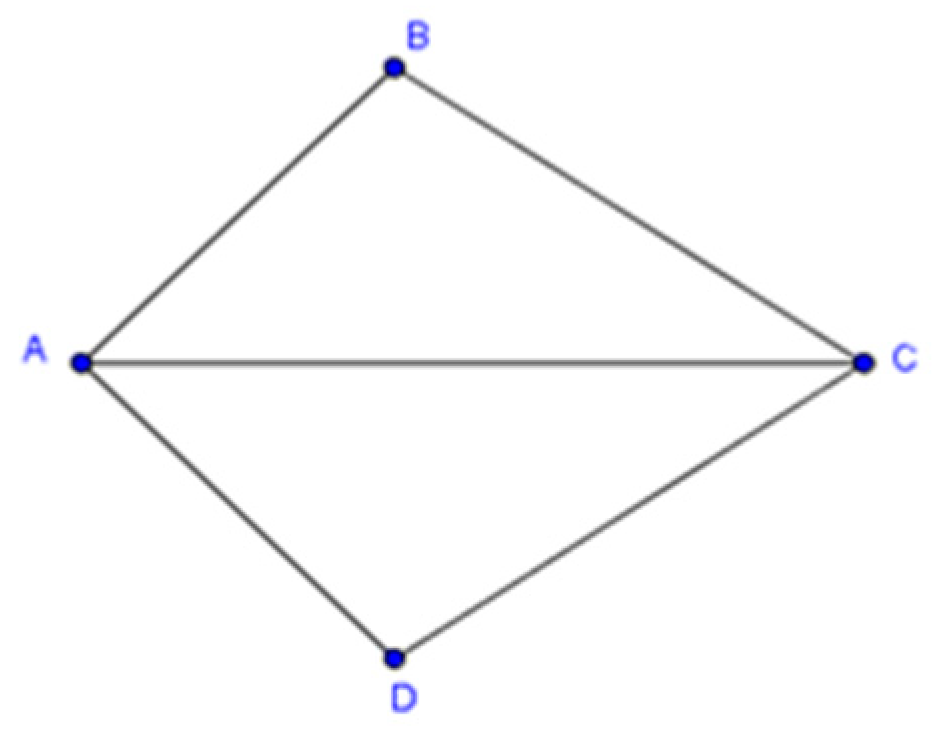
angle B is congruent to angle D
500
What does "CPCTC? stand for?
Corresponding Parts of Congruent Triangles are Congruent