Linear Systems
Quadratic Expressions and Relations
Quadratic Equations
Trigonometry
100
In the form y=mx+b what is the equation when the slope is 6 and the y intercept is 2
y=6x+2
100
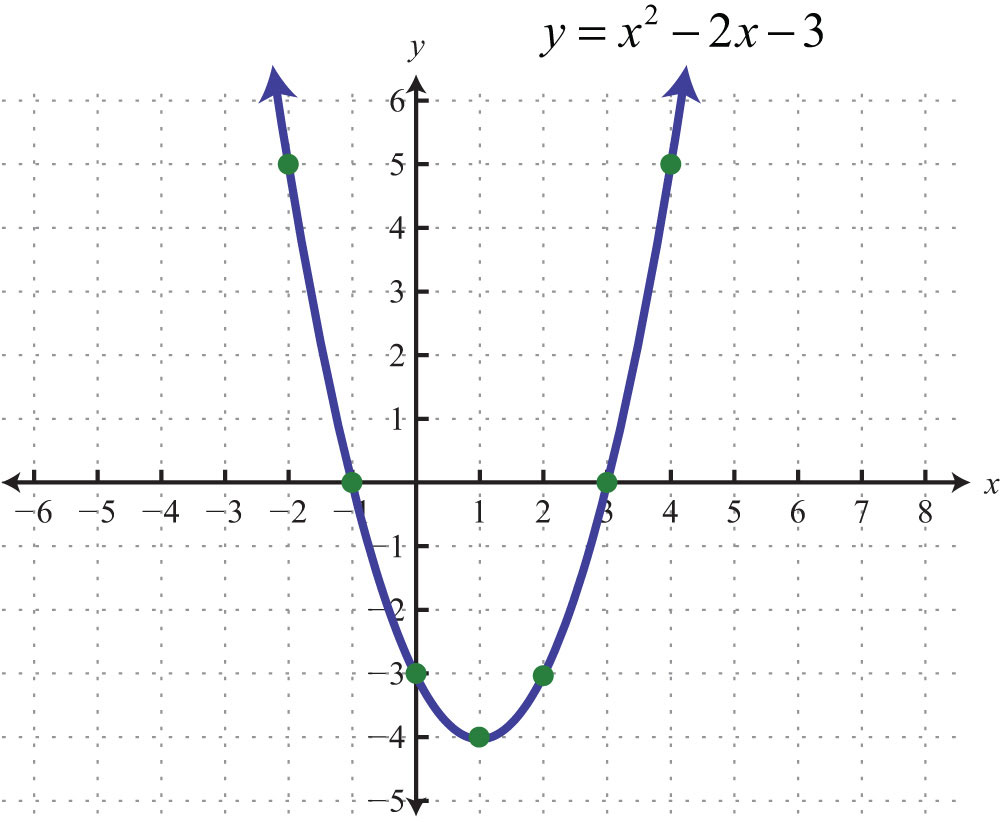Find the domain and range of this parabola
x ∈ R
{ y ∈ R | y ≥ -4 }
100
Using the Zero Product Property to solve the following quadratic equation. (x - 3)(x + 8) = 0
x - 3 = 0 ---> x = 3
x + 8= 0 ---> x = -8
100
Rounded to the nearest hundredth what is cos38o
0.96
200
Solve the following linear system by using Substitution
5x + y =10
10x - y = 5
Finding X Finding Y
y= -5x + 10 y = -5 (1) + 10
10x - y = 5 y = -5 + 10
10x - (-5x + 10) = 5 y = 5
10x + 5x - 10 = 5 x=1 and y= 5
15x = 5 + 10
15x = 15
x = 1
200
Expand the following using foil (x+3)(x+7)
= x2 + 7x + 3x + 21
= x2 + 10x + 21
200
Solve the following quadratic equation by factoring
n2 + 8n = −15
a=1 b=8 c= 15 5 + 3 =8 5 x 3 =15
n2 + 8n +15 = 0
n2 + 5n + 3n +15 = 0
(n2 +5n) + (3n +15) = 0
n(n + 5) + 3(n + 5) =0
n + 3 = 0 ---> n1 = -3
n + 5 = 0 ---> n2 = -5
200
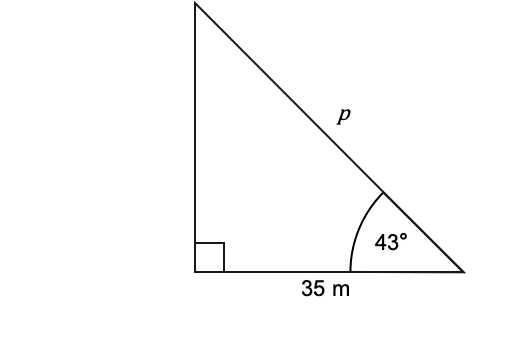Find the Missing side length
Cos43o = A/H
Cos43o = 35/H
0.55 = 35/H
0.55H = 35
H = 35/0.55
H = 63
300
Solve the following linear system by using elimination
−4x + 9y = 9
x − 3y = −6
Solving for Y Solving for X
-4x + 9y = 9 x - 3y = -6
4x + 12y = -24 x - 3(5) = -6
-3y = -15 x - 15 = -6
y = 5 x = -6 + 15
x = 9
x = 9 and y = 5
300
Factor the following Expression Fully if possible
8x2 - 11x + 3
a= 8 b=-11 c= 3 ac= 24
-8 + -3 = -11
-8 + -3 = -24
8x2 -11x +3
=(8x2 -3x)(-8x +3)
=x(8x-3) -1(8x - 3)
=(8x - 3) ( x - 1)
300
Solve the following equation using the Quadratic Formula
2x2 + 2x − 12 = 0
x = (-b ± √b2 - 4ac)/2a
x = (-2 ± √22 - 4(2)(-12))/2(2)
x = (-2 ± √1 - 4(-24))/4
x = (-2 ± √4 + 24)/4
x = (-2 ± √100)/4
x = (-2 ± 10)/4
x1 = (-2 - 10)/4
x1 = (-12)/4
x1 = -3
x2 = (-2 + 10)/4
x2 = (8)/4
x2 = 2
Therefore x1=-3 and x2= 2
300
x/sin80o = 7/Sin60o
x/0.98 = 7/ 0.86
x = (7 x 0.98)/0.86
x = 7.9
x = 8
400
Solve the following Linear System using substitution
-3x + 3y = 4
-x + y = 3
There is No solution
400
State the Specifics and Transformations of the Quadratic Expression
y = 1/5(x + 5)2 + 8
Specifics
Direction of Opening: UP
Max/Min: MIN
Vertex: (-5,8)
Optimal Value: 8
AOS: x=-5
Y-intercept: 13
Transformations
Compressed by a factor of 1/5
Shifted 5 units to the left
Shifted 8 units up
400
Expand, Simplify and solve using the quadratic formula round to the nearest whole number if necessary
(k - 10)(k + 2)
(k + 10)(k - 2)
= k2 - 2k + 10k - 20
= k2 + 8k - 20
a = 1 b= 8 c =-20
x= (-b ± √b2 - 4ac)/2a
x= (-8 ± √82 - 4(1)(-20))/2(1)
x= (-8 ± √82 + 80)/2
x= (-8 ± √64 + 80)/2
x= (-8 ± √144)/2
x= ( -8 ± 12)/2
x1= (-8 + 12)/2 x2= (-8 - 12)/2
x1= 4/2 x2= -20/2
x1= 3.48 x2= -10
x1= 2
400
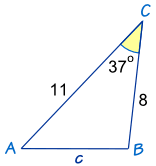Find side C using Cosines Law round to the nearest whole number if necessary
c2= a2 + b2 − 2ab cosC
c2 = 82 + 112 − 2 × 8 × 11 × cos37º
c2 = 64 + 121 − 176 × 0.79
c2 = 45.96
√c2 = √45.96
c = 6.77
c = 7
500
You saved up some money after working for a few months. Yo now $3000 to invest, and you've decided to put some of the money in BMO which is offering a 3% interest, and the rest of the money in TD which is offering a 4% interest. If the total amount of interest you earn for both banks is $65 how much money did you put in each bank.
Let X be the amount of money you put in BMO
Let Y be the amount of money you put in TD
L1x + y = 3000 L2(.03x + 0.04y = 65) x 100
Finding Y Finding X
x + y = 3000 x + y = 3000
3x + 4y = 6500 x + 2500 = 3000
3x + 3y = 9000 x= 3000-2500
3x + 4y = 6500 x = 500
y = 2500 Therefore you put $2500 in TD and 500 in BMO
500
Write an equation in STANDARD FORM for the quadratic relation which results from each transformation and specific
Reflected on the x-axis
Stretched by a factor of six
Shifted 4 units left
Shifted 2 units up
Direction of opening: down
Vertex: (-4,2)
Max/Min: Max
Y intercept: -94
Optimal Value: 2
AOS: x= -4
y= -6x2 - 45x - 94
500
A ball is thrown into the air from a window of a apartment and falls to the ground. The height of the ball is represented by h meters and the time the ball is in the air is represented by t seconds. After the ball is thrown you are given this formula h =4x2 + 17x - 15= 0 How long does it take for the ball to hit the ground. Round the the nearest hundredth if necessary.
a=4 b=17 c=-15
x= (-b ± √b2 -4ac)/2a
x= (-17 ± √172 -4(4)(-15))/2(4)
x= (-17 ± √289 + 240)/8
x= (-17 ± √529)/8
x1= (-17 + 23 )/8 x2 = (-17 - 23)/8
x1 = 6/8 x2 = -40/8
x1 = 0.75 x2 = -5
it will take 0.75 seconds for the ball to hit the ground
500
Tom looks up at the top of a building at an angle of elevation of 62.8o. He looks down at the bottom of the building at an angle of depression of 37.9o. If Tom is standing 10 meters away from the building. How tall is the building?
Tan62.8o = O/A Tan37.9o = O/A
1.94 = O/10 0.77 = O/10
19.4 = O 7.7 = O
19.4 + 7.7 = 27.1 Therefore the building is 27.1 Meters tall