Identify whether the graph of
"y= -3x2 + 6x + 2"
is linear or non-linear
Non-linear. The equation represents a quadratic, non-linear relation.
What is the name of the shape of a quadratic graph?
The shape is called a parabola
What transformation does the "k" value in "y = (x - h)2 + k" represent?
The k value represents a vertical shift: if k>0, the graph shifts up; if k<0, it shifts down.
What is the step pattern using the variable "a"
1a, 3a, 5a, 7a, ...
Find the zeros of
"y = (x−2)(x+5)"
The zeros are x = 2 and x = -5.
Complete the differences table below, and determine the type of relation and why.
x y First diff Second diff
-2 8 - -
-1 6 - -
0 4 - -
1 2 - -
2 0 - -
Linear because the 1st diff are the same
x y First diff Second diff
-2 8 -2 0
-1 6 -2 0
0 4 -2 0
1 2 -2
2 0
Find the vertex of
"y = (x - 2)2 + 3"
The vertex is (2, 3).
What transformation does the "h" value in "y = (x - h)2 + k" represent?
The h value represents a horizontal shift: if h>0, the graph shifts right; if h<0, it shifts left.
Write how the x and y values are transformed in mapping notation. (Hint: the second table)
x+h, ay+k
How can the axis of symmetry be used to help find the vertex?
sub in the midpoint value (axis of symmetry) for x into the relation
Complete the differences table below, and determine the type of relation and why.
x y First diff Second diff
0 33.5 - -
2 9.5 - -
4 -2.5 - -
6 -2.5 - -
8 9.5 - -
Quadratic because the 2nd diff are the same
x y First diff Second diff
0 33.5 -24 12
2 9.5 -12 12
4 -2.5 0 12
6 -2.5 12
8 9.5
Describe what the value of "a" in
"y= ax2 + bx + c"
tells you about the direction of the graph's opening.
The value of "a" tells you whether the parabola opens upward (if a>0) or downward (if a<0).
Describe the transformations in
"y = 3(x - 2)2 + 5"
compared to the parent function "y = x2"
Shifted right by 2 units (because h=2).
Shifted up by 5 units (because k=5).
Vertically stretched bafo 3 (because a=3).
If "a = −3" in
"y = a(x - 2)2 - 1"
describe the steps to graph it starting from the vertex, and explain the changes in the parabola’s shape.
The vertex is (2, -1). The step pattern is -3, -9, -15. Start from (2, -1) and apply the reflected, stretched step pattern.
Given "y = (x−1)(x+4)"
find its zeros and vertex, and graph the equation.
Zeros: x=1, x=−4.
Axis of symmetry: halfway between the zeros, x=−1.5.
Vertex: (−1.5,−6.25).
Complete the differences table below, and determine the type of relation and why.
x y First diff Second diff
-3 0 - -
-2 4 - -
-1 5 - -
0 7 - -
1 10 - -
2 14 - -
3 15 - -
Neither because the 1st and 2nd diff are not the same
x y First diff Second diff
-3 0 4 -3
-2 4 1 1
-1 5 2 1
0 7 3 1
1 10 4 -3
2 14 1
3 15
Find the axis of symmetry and vertex for
"y = -2(x + 4)2 + 5"
and explain what the graph looks like.
The axis of symmetry is x=−4.
The vertex is (-4,5).
The parabola opens downward and is vertically stretched by a factor of 2.
Describe the transformations of
"y = -2(x + 3)2 - 4"
compared to the parent function "y = x2"
Reflected on the x-axis (because a=−2).
Vertically stretched bafo of 2.
Shifted left by 3 units (because h=−3).
Shifted down by 4 units (because k=−4).
Graph "y = 1/2(x - 1)2 + 3"
using mapping notation. (Specify the second table and how the x and y values are transformed)
x+1, 1/2y+3
x y x+1 1/2y+3
-2 4 -1 5
-1 1 0 3.5
0 0 1 3
1 1 2 3.5
2 4 3 5
Determine the equation, in factored form, for the parabola shown below:
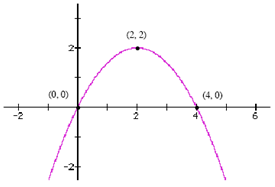
y = a(x-r)(x-s)
y = a(x+0)(x-4)
sub a point from the graph (vertex)
2 = a(2+0)(2-4)
2 = a(2)(-2)
2 = a(-4)
a = -0.5
Therefore: y = -0.5(x)(x-4)