Functions
Rational Expressions
Transformations
Trig(Special Angles)
Trig Functions
Discrete Functions
100
What is the domain of the function:
F(x)=x^2+7x+9
Domain=XER
100
Simplify: (X^2-9)/(x+3)
X-3 (for x cannot equal -3)
100
What is the result of translating ( f(x) = x2) up by 3 units?
F(x)=x^2+3
100
Using Special Triangles. Determine the following:
sin(45)
(1/sqrt2)
100
What is the period of
y=sin(x)
The period is 360∘
100
What is the first term of the sequence t(n)=3n+1?
The first term is 4
200
What is the range of the following function:
f(x)=x^2
Range= Y is an element of real numbers such that y is greater then or equal to 0.
200
Simplify the following:
(X^2-4)/(x^2-x-6)
(X+2)/(x-3)
200
Reflect the function over the X Axis.
f(x)=x^3
f(x)=-x^3
200
What is cos(30)?
(sqrt3)/2
200
What is the amplitude of
y=3sin(2x)
The amplitude is 3
200
Find the sum of the first 5 terms of the arithmetic sequence with first term 2 and common difference 3.
s5=40
300
Given the following: Find (f x g)(x)
F(x)=x^2 and G(x)=2x+3
(f x g)(x)=2x^2+3
300
Add the Following:
frac{2}{x} + \frac{3}{x+1}
frac{2(x+1) + 3x}{x(x+1)} = \frac{5x + 2}{x(x+1)
300
What is the effect of the transformation:
f(x)=2(x−1)^2+3
Vertical stretch by 2, translate right by 1 unit, and up by 3 units
300
What is Tan(60)
sqrt3
300
What is the phase shift of
y=2cos3(x−45∘)+2
The phase shift is 45° to the right
300
What is the 5th term of the geometric sequence with first term 3 and common ratio 2?
s5=48
400
What is the inverse of the function:
f(x)=(3x-2)/4
f^-1(x)=(4x+2)/3
400
Multiply the following:
frac{x^2}{x - 1} \times \frac{x - 1}{x + 2}
frac{x^2}{x + 2}
400
What is the result of reflecting the following function over the x axis:
y=7(x−5)^2
y=-7(x−5)^2
400
Using special triangles, what is sin(60)?
frac(sqrt3)(2)
400
Write the following function as a cosine function:
y=2sin(x)
y=2cos(x−90∘)
400
Determine if the following infinite geometric series converges, if so find the sum.
∑ (n=0) 5(1/3)^n
The Function is converging
The sum of the infinite converging series is 7.5
500
A company’s profit P(x) in thousands of dollars, based on the number of units (x) sold, is given by P(x)=−2x2+8x−6. Find the number of units sold that would result in zero profit.
Factorize the quadratic:
X=1 X=3
Therefore it would take selling 1 or 3 units to have $0 in profit.
500
A tank can be filled by two pipes. Pipe A can fill the tank in ( x )hours, while Pipe B can fill the same tank in ( x + 2 ) hours. If both pipes are opened together, it takes 3 hours to fill the tank. Find the time it takes for each pipe to fill the tank separately.
Pipe A fills the tank in the 6 hours and Pipe B fills the tank in 8 hours.
500
A satellite dish has a parabolic shape and is modeled by the equation y=4(x−3)2+5 Describe the transformations applied to the parent function y=x2 and determine the vertex of the parabola.
The transformation applied to the parent function y=x2 includes a vertical stretch by 4, a translation 3 units to the right, and 5 units up. The vertex of the parabola is at (3,5).
500
A lighthouse casts a shadow creating an angle of elevation of 30° to the top of the lighthouse from a point 100 meters away from the base. Calculate the height of the lighthouse. Round to 2 decimal places.
The height of the lighthouse is 57.74 meters.
500
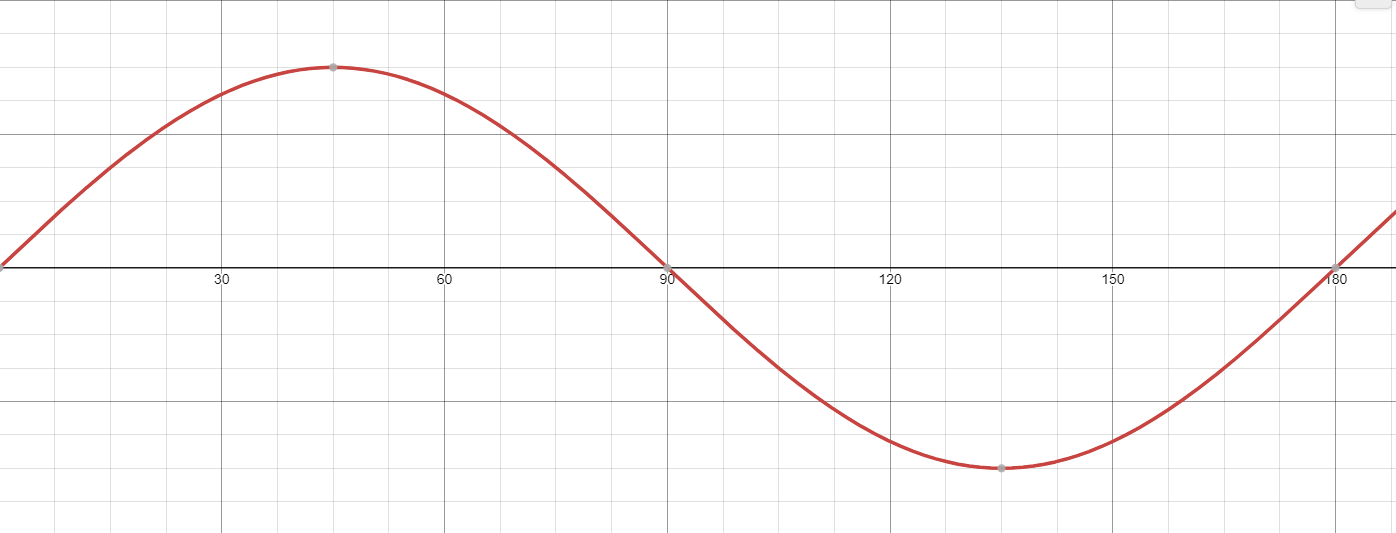
An object moves in simple harmonic motion described by y = 3sin(2x), where x is the time in seconds. Determine the time it takes for the object to return to its Minimum displacement. State the Period. Then graph one cycle.
Period=180. The function will return from its minimum height to zero at 180 degrees.
500
A company offers a promotion where customers receive a 10% discount on their next purchase after each visit. If a customer starts with a $100 purchase, determine the total amount spent after 6 visits.
This problem is an example of a geometric sequence where the first term a=100 and the common ratio r=0.9. The sum of the first 6 terms is $468.56.