Turns
X & Y Intercepts
Random
(Fix, Graph, Create or Extra Info)
(Fix, Graph, Create or Extra Info)
End Behavior
Multiplicity
100
This part of a Polynomial Function helps solve for the amount of "Turns"
Degree of the Polynomial?
100
The Y-Intercept of this Function
-2
100
This part makes a Polynomial Function a Polynomial Function
a function that involves only non-negative integer powers of X
(Simple Answer: All exponents have to be positive)
100
The Definition of End Behavior
It is the behavior of the graph as it approaches positive or negative infinity based on the Degree and Leading Coefficient of a Polynomial Function.
(Simple Answer: The ends of the graph go up or down based on the Degree and Leading Coefficient)
100
The Definition of the word "Multiplicity" in a Polynomial Function
the amount of times a given factor appears in the factored form of the equation of a polynomial
(Simple Answer: Number of same X Values when solving for X-Int)
200
This Polynomial Function has __ number of Turns
f(x)=x3-x2-4x+4
2 Turns?
200
The Definition of X & Y Intercepts
It is the Y-Intercept is the point where the function or graph has an X input value of 0; X-Intercept is a point(s) where the graph crosses or touches the x-axis.
(Simple Answer: Where the line on the graph touches or crosses the X & Y axis on the graph)
200
The maximum number of turning points of a polynomial function of degree 4
3
200
The End Behavior of 2x2+3x+1
"Positive Infinity," "Positive Infinity"
(Simple Answer: End Behavior of "Up," "Up")
200
The Multiplicity of this graph
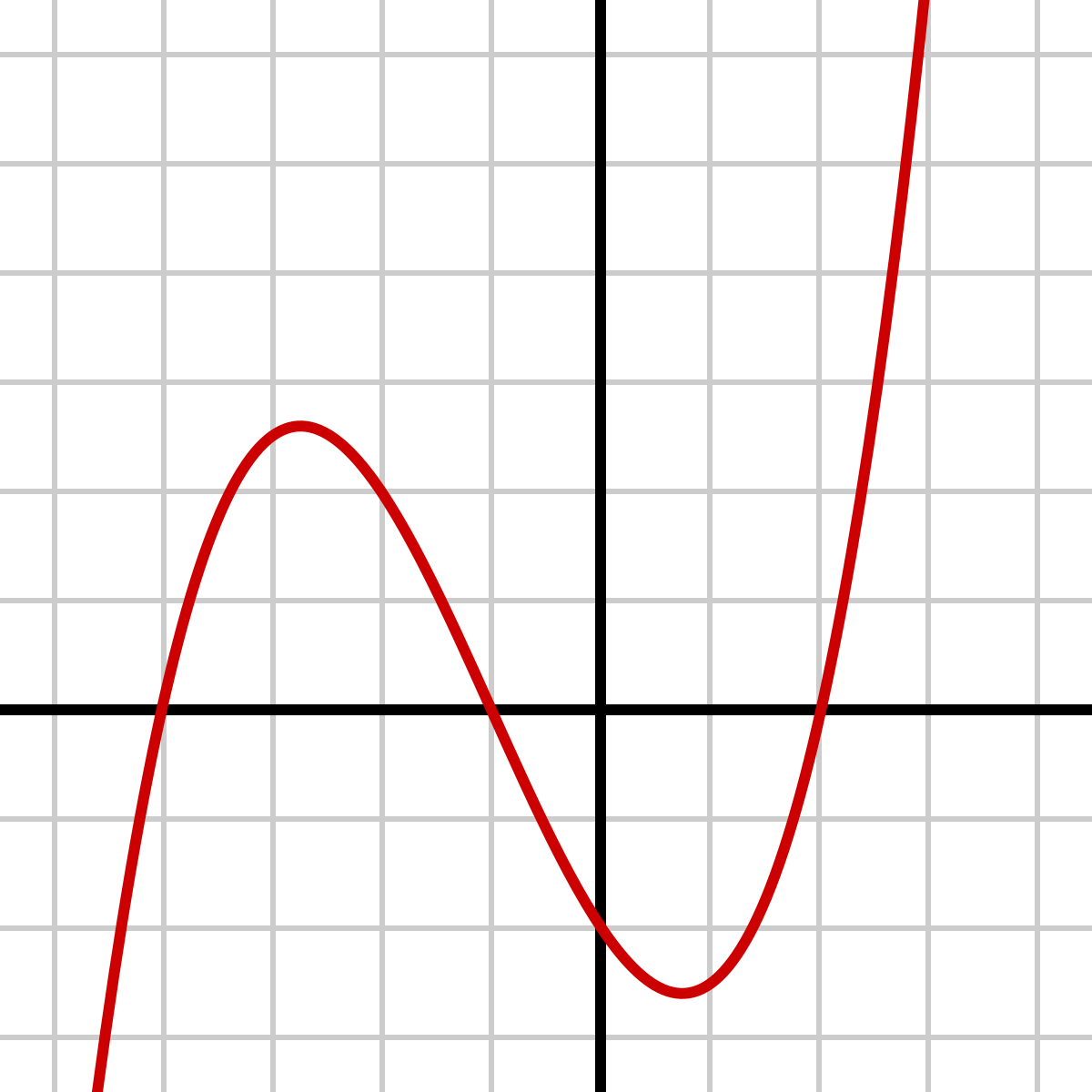
"odd" or "1" Multiplicity
300
The Definition of the word "Turns" in a Polynomial Function
It is where the Polynomial Function Graphed changes from increasing to decreasing or decreasing to increasing.
(Simple Answer: Where the graph goes from up to down or down to up)
300
The correct steps in solving for the X- and Y- Intercepts
What is to find X-Intercepts set "Y" or "f(x)" to 0 and factor; for Y-Intercepts use the term "B" from the line equation y=mx+b?
(Simple Answer: Replace "Y" value with 0 and solve for X; To find the Y-Intercept use the term in the equation that doesn't have a X value)
300
What is the shape of a Quartic Polynomial Function
W-Shape
300
The Proper way to find/determine End Behavior
What is an even degree will either approach negative infinity(Left), negative infinity(Right) or positive infinity(Left), positive infinity(Right) and a odd degree will either approach positive infinity(Left), negative infinity(Right) or negative infinity(Left), positive infinity(Right); A positive Leading Coefficient will cause the left side of the graph to reach positive infinity and vise versa for a negative Leading Coefficient?
(Simple Answer: A positive LC (Leading Coefficient) will cause the left side of the graph to rise up and a negative LC will cause the left side to fall down; the right side of the graph is determined by the degree and if its even it will copy the left side and if odd it will be shaped opposite)
300
These different types of Multiplicity cause the graph to do this
an "odd" multiplicity causes the graph to cross the x-axis and an "even" multiplicity will rebound off the x-axis
(Simple Answer: "Odd" or "1" multiplicity will go through the x-axis and "Even" or "2" multiplicity "bounces off" or "doesn't cross" the x-axis)
400
This Polynomial Function has __ number of Turns
f(x)=-9x5+54x3-81x
4
400
The X-Intercept(s) of this Function
f(x)=-x3-6x2+16x
(-8,0), (2,0), & (0,0)
400
Is there a zero of multiplicity 2 in the function
f(x)=-x3-6x2+16x?
Yes
400
The End Behavior of this Polynomial Function
f(x)=-x4+11x2-10
"Negative Infinity," "Negative Infinity" End Behavior
(Simple Answer: An End Behavior of "Down," "Down")
400
What are the intercepts of the following function?
f(x)=-x4-3x3+4x2
(0,0), (0,0), (-4,0), (1,0)
500
This Polynomial Function has __ number of Turns
(List and Draw the rough shape with proper number of Turns of the Function. (End Behavior, X & Y-Intercepts, etc doesn't matter for this exercise)
f(x)=x3+3x2-4x-12
2
500
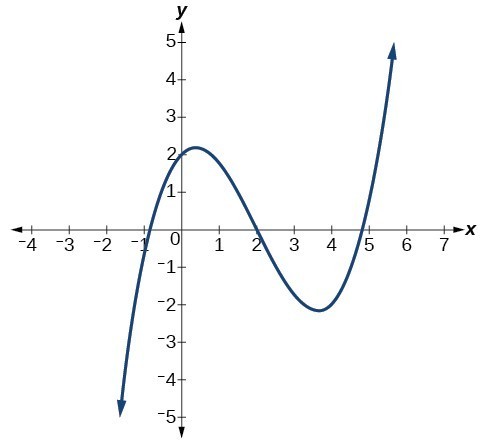
The X & Y Intercept(s) of this Function
f(x)=-x4-3x3+4x2
(-4,0), (1,0), (0,0) & (0,0)
(Explanation: There is a Y-intercept of "0" because the function doesn't have a "b" term (a.k.a no term without a X value). The X-intercepts are factored like normal but there are two X-intercepts of the same due to factoring giving a function of x2=0 (This is what gives you two of the same answers).
500
What Polynomial Function has the following conditions:
End Behavior: (Positive Infinity, Positive Infinity)
X-Intercepts: ("2" X-Intercepts)
Y-Intercepts: (0,-1)
Turns: (1)
Multiplicity: ("1" or "odd")
f(x)=2x2+3x+1
500
The End Behavior of the following Polynomial Function
(List and Draw the End Behavior of the Polynomial Function. (All other variables for graphing polynomials is not required for this exercise)
f(x)=x3-x2-4x+4
"Negative Infinity, Positive Infinity" End Behavior
(Simple Answer: An End Behavior of "Down," "Up")
500
This Polynomial Function has a Multiplicity of __
f(x)=-9x5+54x3-81x
Multiplicity of "2"
(Explanation: The "duplicate" factors of "ā3" & "iā3" is what gives the multiplicity of "2" because there is two per factor)
