(Fix, Graph, Create or Extra Info)
This part of a Polynomial Function helps solve for the amount of "Turns"
What is the "Degree" of the Polynomial?
The Y-Intercept of this Function

What is a Y-Intercept of "-2"?
This part makes a Polynomial Function a Polynomial Function
What is "a function that involves only non-negative integer powers of X"?
(Simple Answer: All exponents have to be positive)
The Definition of End Behavior
What is the behavior of the graph as it approaches positive or negative infinity based on the Degree and Leading Coefficient of a Polynomial Function?
(Simple Answer: The ends of the graph go up or down based on the Degree and Leading Coefficient)
The Definition of the word "Multiplicity" in a Polynomial Function
What is the amount of times a given factor appears in the factored form of the equation of a polynomial?
(Simple Answer: Number of same X Values when solving for X-Int)
This Polynomial Function has __ number of Turns
f(x)=x3-x2-4x+4
What is "2" Turns?
The Definition of X & Y Intercepts
What is the Y-Intercept is the point where the function or graph has an X input value of 0; X-Intercept is a point(s) where the graph crosses or touches the x-axis?
(Simple Answer: Where the line on the graph touches or crosses the X & Y axis on the graph)
The Proper Graph for the Polynomial Function f(x)=x4-7x2+10
(Choose the Correct Graph)
A:
B:
What is Graph "A"?
The End Behavior of 2x2+3x+1
What is "Positive Infinity," "Positive Infinity"?
(Simple Answer: End Behavior of "Up," "Up")

The Multiplicity of this graph
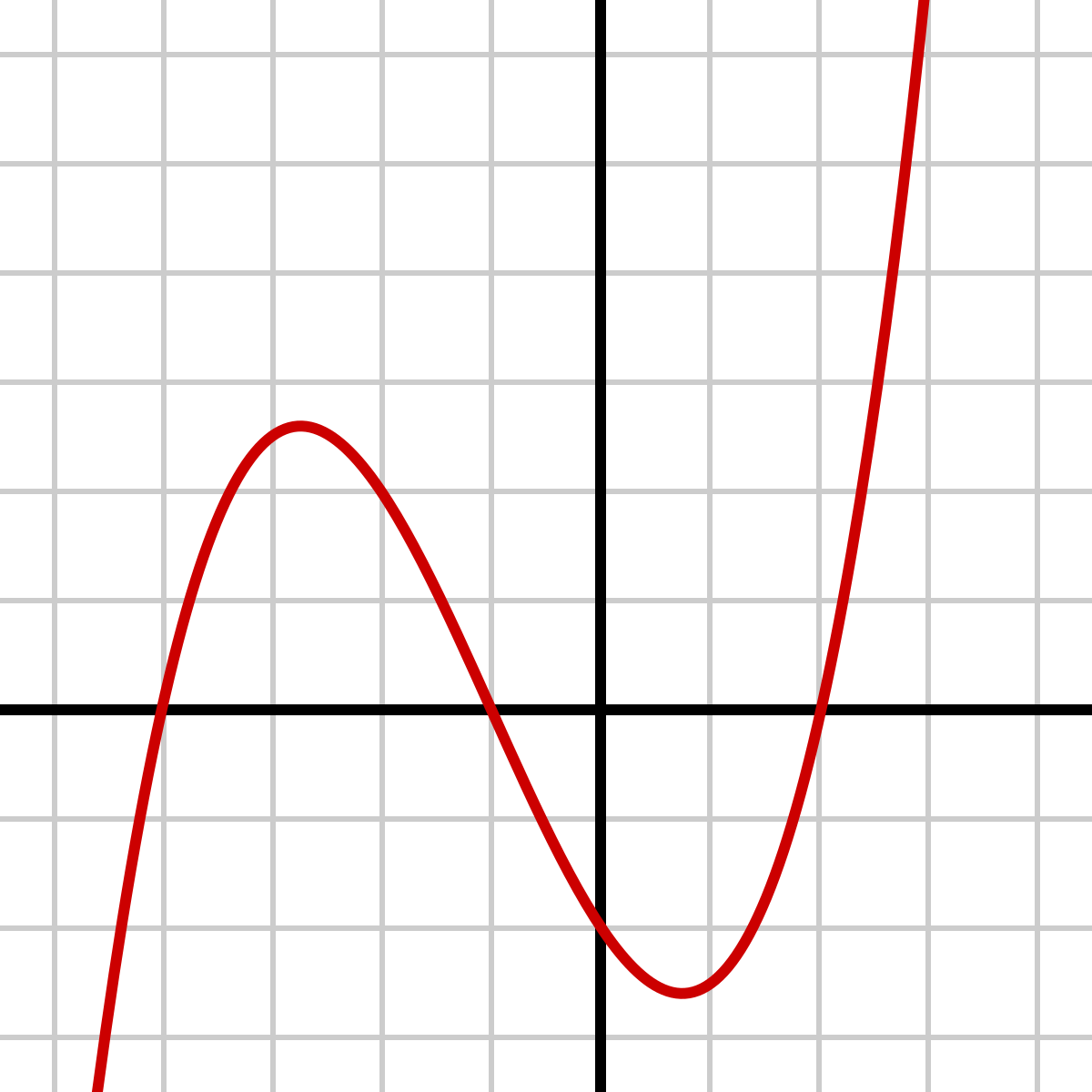
What is an "odd" or "1" Multiplicity?
The Definition of the word "Turns" in a Polynomial Function
What is where the Polynomial Function Graphed changes from increasing to decreasing or decreasing to increasing?
(Simple Answer: Where the graph goes from up to down or down to up)
The correct steps to finding X & Y Intercepts
What is to find X-Intercepts set "Y" or "f(x)" to 0 and factor; for Y-Intercepts use the term "B" from the line equation y=mx+b?
(Simple Answer: Replace "Y" value with 0 and solve for X; To find the Y-Intercept use the term in the equation that doesn't have a X value)
These are the 5 Shapes of a Polynomial Function
What is:
0 is Constant w/ Shape Point
1 is Linear w/ Shape Line
2 is Quadratic w/ Shape Parabola
3 is Cubic w/ Shape S-Shape
4 is Quartic w/ Shape W-Shape
The Proper way to find/determine End Behavior
What is an even degree will either approach negative infinity(Left), negative infinity(Right) or positive infinity(Left), positive infinity(Right) and a odd degree will either approach positive infinity(Left), negative infinity(Right) or negative infinity(Left), positive infinity(Right); A positive Leading Coefficient will cause the left side of the graph to reach positive infinity and vise versa for a negative Leading Coefficient?
(Simple Answer: A positive LC (Leading Coefficient) will cause the left side of the graph to rise up and a negative LC will cause the left side to fall down; the right side of the graph is determined by the degree and if its even it will copy the left side and if odd it will be shaped opposite)
These different types of Multiplicity cause the graph to do this
What is an "odd" multiplicity causes the graph to cross the x-axis and an "even" multiplicity will rebound off the x-axis?
(Simple Answer: "Odd" or "1" multiplicity will go through the x-axis and "Even" or "2" multiplicity "bounces off" or "doesn't cross" the x-axis)
This Polynomial Function has __ number of Turns
f(x)=-9x5+54x3-81x
What is "4" Turns?
The X-Intercept(s) of this Function
f(x)=-x3-6x2+16x
What is: (-8,0), (2,0), & (0,0)?
Gabriel is graphing the function f(x)=-x3-6x2+16x.
(Identify and Fix the Graph (There is ONE specific problem causing multiple issues with the graph)
What is a problem of an "Even Multiplicity"?
(Gabriel has the correct X-Intercepts but has drawn the graph with a multiplicity of "2" causing the Multiplicity, Turns & End Behavior to be wrong)
The End Behavior of this Polynomial Function
f(x)=-x4+11x2-10
What is a "Negative Infinity," "Negative Infinity" End Behavior?
(Simple Answer: An End Behavior of "Down," "Down")
This Polynomial Function has a __ Multiplicity
(List given factors of the equation)
f(x)=-x4-3x3+4x2
What is a Multiplicity of "2" with given factors of (0,0), (0,0), (-4,0), (1,0)?
(Explanation: The "duplicate" factors of "(0,0)" is what gives the multiplicity of "2" because there is two of them)
This Polynomial Function has __ number of Turns
(List and Draw the rough shape with proper number of Turns of the Function. (End Behavior, X & Y-Intercepts, etc doesn't matter for this exercise)
f(x)=x3+3x2-4x-12
What is "2" Turns?
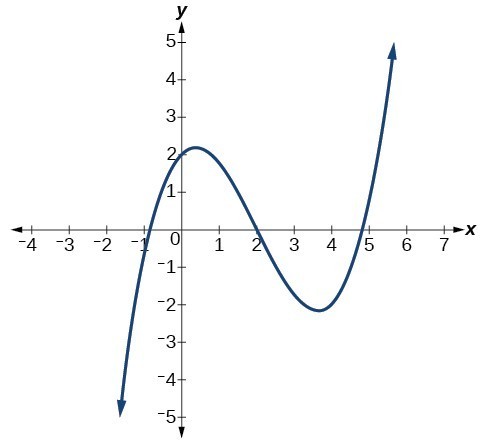
The X & Y Intercept(s) of this Function
f(x)=-x4-3x3+4x2
What is a Y-Intercept of 0 and X-Intercepts of (-4,0), (1,0), (0,0) & (0,0)?
(Explanation: There is a Y-intercept of "0" because the function doesn't have a "b" term (a.k.a no term without a X value). The X-intercepts are factored like normal but there are two X-intercepts of the same due to factoring giving a function of x2=0 (This is what gives you two of the same answers).
Create and Graph a Polynomial Function with the following restraints:
End Behavior: (Positive Infinity, Positive Infinity)
X-Intercepts: ("2" X-Intercepts)
Y-Intercepts: (0,-1)
Turns: (1)
Multiplicity: ("1" or "odd")
What is f(x)=2x2+3x+1
Graph:
The End Behavior of the following Polynomial Function
(List and Draw the End Behavior of the Polynomial Function. (All other variables for graphing polynomials is not required for this exercise)
f(x)=x3-x2-4x+4
What is "Negative Infinity, Positive Infinity" End Behavior?
(Simple Answer: An End Behavior of "Down," "Up")

This Polynomial Function has a Multiplicity of __
(List and Draw the Multiplicity of the Polynomial Function. (All other variables for graphing the polynomials is not required for this exercise)
f(x)=-9x5+54x3-81x
What is a Multiplicity of "2" with given factors of (0,0), √3, √3, i√3, i√3?
(Explanation: The "duplicate" factors of "√3" & "i√3" is what gives the multiplicity of "2" because there is two per factor)