In Vertex form the equation is f(x) = +/-a(x-h)^2 + k.
What transformations does the - cause?
What is Reflection
If a toy rocket is launched vertically upward with an initial velocity of 75 feet per second, then its height h after t seconds is given by the equation h(t) = -16t^2 + 75t. Find the Rocket's starting height.
0 feet
Name the x-intercepts. y=-(x - 3)^2 + 1
What is (2,0) and (4,0)
Name the vertex.
What is (-3, -2)?
In Vertex form the equation is f(x) = +/-a(x-h)^2 + k.
What transformations does the h cause?
What is translation left or right
If a toy rocket is launched vertically upward from ground level with an initial velocity of 75 feet per second, then its height h after t seconds is given by the equation h(t) = -16t^2 + 75t. Find when the rocket will hit the ground.
What is 4.69 Seconds
Name the x-intercepts. Y=2x^2 - 12x + 10
What is (1,0) and (5,0)
Name the vertex.
f(x) = (x+1)^2 - 8
What is (-1, -8)?
In Vertex form the equation is f(x) = +/-a(x-h)^2 + k.
What transformations does the k cause?
translation up or down.
If a toy rocket is launched vertically upward from ground level with an initial velocity of 75 feet per second, then its height h after t seconds is given by the equation h(t) = -16t^2 + 75t. Find the maximum height of the rocket.
What is 87.89 feet
Name the y-intercepts. y=(x + 2)^2 + 3
What is (0,7)
Name the vertex.
f(x) = (x-3)^2 +4
What is (3,4)?
In Vertex form the equation is f(x) = +/-a(x-h)^2 + k.
What transformations does the a cause?
What is a vertical stretch or shrink
If a toy rocket is launched vertically upward from ground level with an initial velocity of 75 feet per second, then its height h after t seconds is given by the equation h(t) = -16t^2 + 75t. Find when the rocket be 44 feet in the air.
What is 4 seconds.
Name the x-intercepts y=x^2 - x - 2
What is (-1,0) and (2,0)?
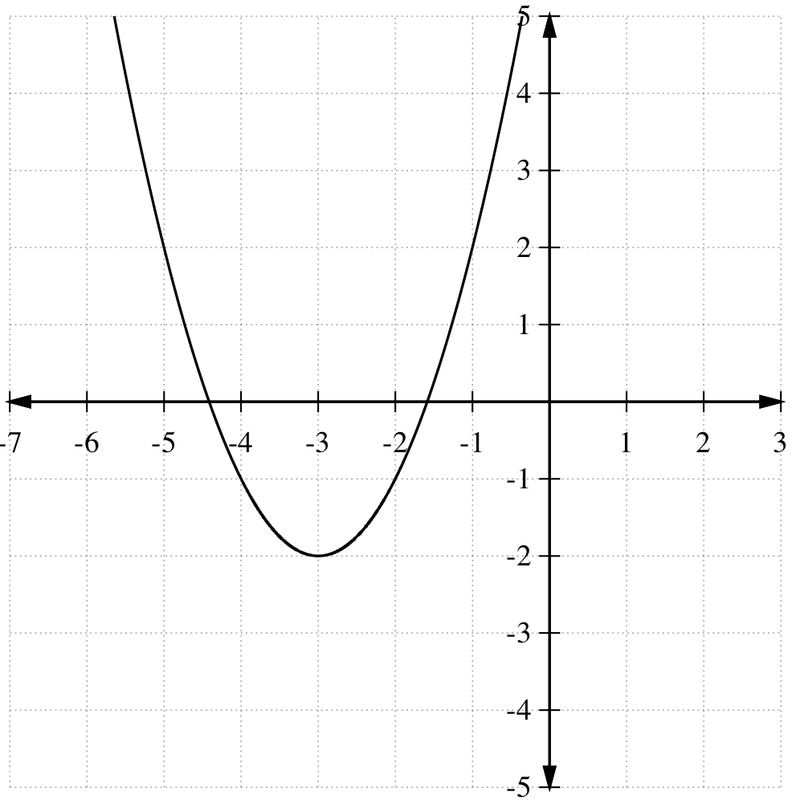
Name the vertex.
f(x) = x^2 - 4x - 5
What is (2,-9)?
Name all the transformations on this function.
f(x) = - 5/3 (x - 6)^2 + 2
What is:
Reflection
Vertical stretch
Translation right 6
Translation up 2
If a toy rocket is launched vertically upward from ground level with an initial velocity of 75 feet per second, then its height h after t seconds is given by the equation h(t) = -16t^2 + 75t. His brother climbs a tree right behind him and fires a rocket from a branch above him, then its height h after t seconds is given by the equation h(t) = -16t^2 + 60t + 10. Find when the rockets will collide.
0.67 seconds.
Name the vertex.
f(x) = 2x^2 + 4x - 6
What is (-1,-8)?