Transformations
Graphing & Key features!
Writing Factored Form
Writing Regressions & Projectiles!
Writing Vertex Form & Standard Form
100
What is the value of n, if f(x)=x2 +k
k=4
100
Graph y=(x+4)2-1, and identify these key features:
- vertex
-axis of symmetry
-domain & Range
-y-intercept
-solutions
-how many solutions
- vertex: (-4,-1)
-axis of symmetry
x=-4
-domain & Range:
D: all real numbers
R:
y>=-1
-y-intercept (0,15)
-solutions (-5,0) (-3,0)
-how many solutions 2
100
A parabola passes through the point (-2,60) and has roots at ( -4,0) and (3,0), what is the equation in factored form?
y=-6(x-3)(x+4)
100
Company X tried selling widgets at various prices to see how much profit they would make. The following table shows the widget selling price, x, and the total profit earned at that price, y. Write a quadratic regression equation for this set of data, rounding all coefficients to the nearest tenth.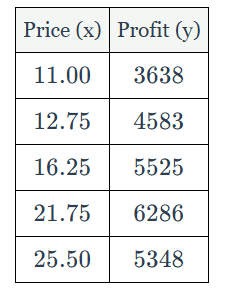 
y = − 29 x ^2 + 1182.3 x − 5849.6
100
Write the equation of the given graph in VERTEX FORM.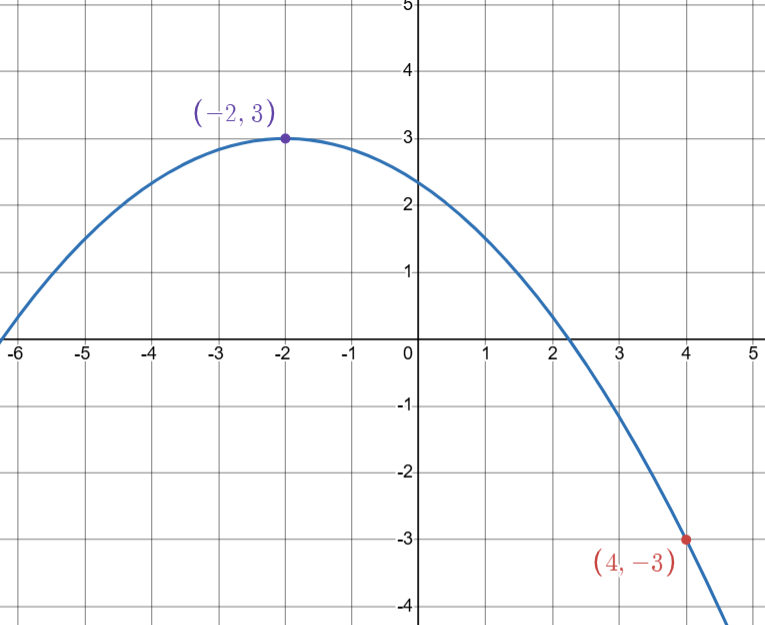 
y=-\frac{1}{6}(x+2)^{2}+3
200
What is the equation of the quadratic that was vertically stretched by a factor of 2, shifted to the right by 3 and shifted down by 5 units?
y=2(x-3)2-5
200
Graph
y=-1/2(x-5)^2-2, and identify these key features:
- vertex
-axis of symmetry
-domain & Range
-y-intercept
-solutions
-how many solutions
(5,-2) x=5
Domain: All real numbers
Range: y<=-2
Y-intercept (0,-14.5)
Solutions: NONE
How many? ZERO
200
A parabola passes through the point (1,144) and has roots at ( -1,0) and (9,0), what is the equation in factored form?
y=-9(x+1)(x-9)
200
A rocket is shot off from a launcher. The accompanying table represents the height of the rocket at given times, where x is time, in seconds, and y is height, in feet. Write a quadratic regression equation for this set of data, rounding all coefficients to the nearest hundredth.
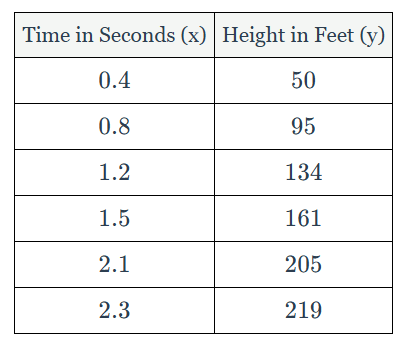
y=−14.96x ^2 +128.92x+1.04
200
Write an equation in VERTEX form of the quadratic function whose vertex is (2,-4) and passes through the point (6,4).
y=\frac{1}{2}(x-2)^{2}-4
300
Identify the transformations in the equation:
y=-3(x+4)2+5
Reflection across the x-axis
Vertically stretched by a factor of 3
Shifted to the left by 4
Shifted up by 5
300
Graph and identify these key features,
y=3/4(x+6)^2-3
- vertex
-axis of symmetry
-domain & Range
-y-intercept
-solutions
-how many solutions
(-6,-3) x=-6
D: all real numbers
R: y>=-3
(0,24)
(-8,0) and ( -4,0)
2 solutions
300
A parabola passes through the point (5,-24) and has roots at ( -4,0) and (-3,0), what is the equation in factored form?
y=-\frac{1}{3}(x+3)(x+4)
300
A rocket is shot off from a launcher. The accompanying table represents the height of the rocket at given times, where x is time, in seconds, and y is height, in feet. Write a quadratic regression equation for this set of data, rounding to the nearest tenth. With the equation find the maximum height of the rocket
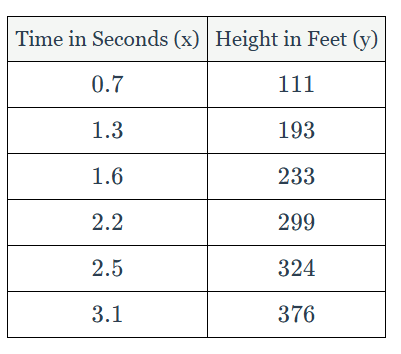
y=−15.9x ^2 +170.5x−0.6
max. height of 456.5
300
Write an equation in VERTEX form of the quadratic function whose vertex is (2,-4) and passes through the point (6,-8).
y=-\frac{1}{4}(x-2)^{2}-4
400
Identify the transformations of the equation:
y=1/2(x+4)2-7
Vertically compressed by a factor of 1/2
Shifted to the left by 4
Shifted down by 7
400
Graph and identify these key features,
y=-2x^{2}+6x+3
- vertex
-axis of symmetry
-domain & Range
-y-intercept
-solutions
-how many solutions
(1.5, 7.5) x=1.5
D: all real numbers
R: y<=7.5
(-.44, 0) and (3.44,0)
2 solutions
400
A parabola passes through the point (8,-8) and has roots at ( -2,0) and (4,0), what is the equation in factored form?
y=-\frac{1}{5}(x+2)(x-4)
400
A rocket is shot off from a launcher on a wooden platform, which is represented by the equation below. When does the rocket hit the ground? At what height is platform the rocket is being shot off? (time & feet)
y=-23x^{2}+39x+3
Hits the ground @ 1.77 seconds.
The platform is 3 feet off the ground.
400
Write an equation in STANDARD form of the quadratic function whose vertex is (-1,4) and passes through the point (1,12).
y=2x^{2}+4x+6
500
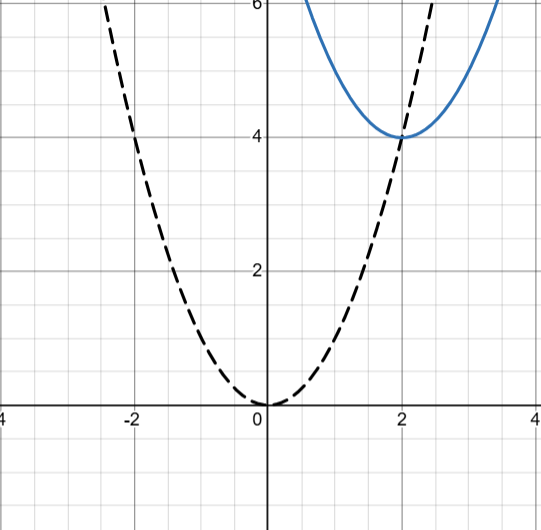
The graph of the quadratic functions f(x) and g(x) are shown. if f(x)=x2 and g(x)=f(x+a)2+b, what is the value of b?
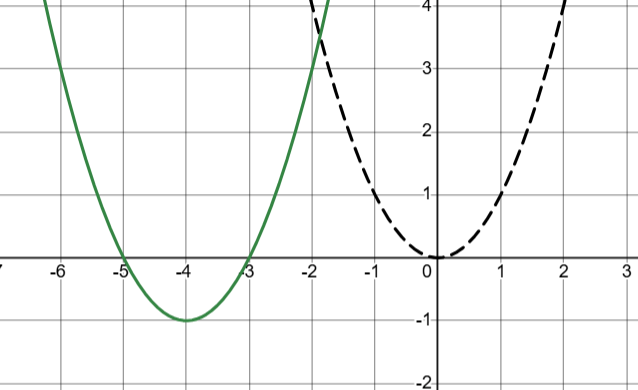
b=-1
500
Graph and identify these key features,
y=1/3x^{2}-6x
- vertex
-axis of symmetry
-domain & Range
-y-intercept
-solutions
-how many solutions
(9,-27) x=9
D: all real numbers
R: y>=-27
(0,0)
(0,0) & (18,0)
2 solutions
500
A parabola passes through the point (10,-14) and has roots at ( -2,0) and (3,0), what is the equation in factored form?
y=-\frac{1}{6}(x+2)(x-3)
500
A rocket is shot off from a launcher on a wooden platform, which is represented by the equation below. When does the rocket hit the ground? What is the maximum height of the rocket? What is the height of the rocket at 1.3 seconds?
Hits the ground at 2.19 seconds
Max. Height of the rocket is 30 feet.
Height 27.84 feet
500
Write an equation in STANDARD form of the quadratic function whose vertex is (0.5,3) and passes through the point (-2,-22).
y=-4x^{2}+4x+2