5.1
5.2
5.3
100
Wat is de belangrijkste eigenschap van een driehoek als je de stelling van Pythagoras wilt gebruiken?
Er moet een hoek van 90o inzitten.
(moet een rechthoekige driehoek zijn)
100
Bereken LM op 1 decimaal nauwkeurig.
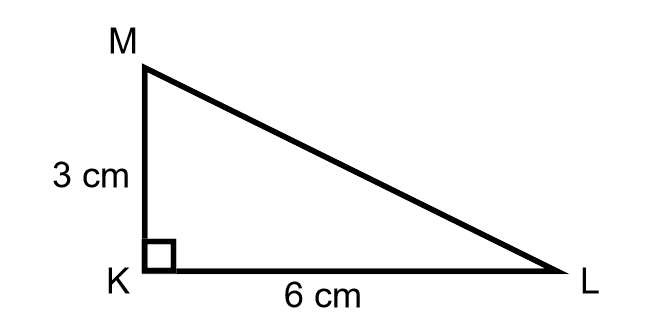
KL is schuine zijde
KL² = 3² +6² = 9 + 36 = 45
KL = sqrt45=6,70..
KL =6,7 cm
100
Wat moet je tekenen in bijv. een trapezium om de gevraagde zijde te kunnen berekenen? En waarom?
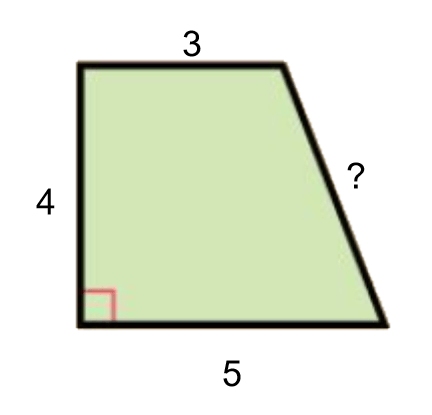
een hulplijn, zodat je een rechthoekige driehoek hebt waarin je de stelling van pythagoras kunt toepassen.
200
Wat kun je zeggen over de oppervlakte van vierkant 3?
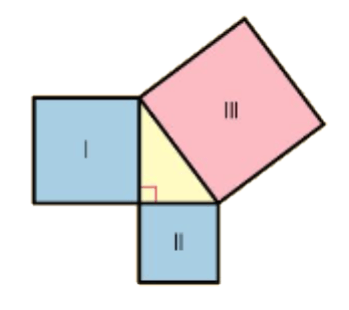
de oppervlakte van vierkant 3 is de oppervlakte van vierkant 1 en vierkant 2 opgeteld.
200
Bereken LM op 1 decimaal nauwkeurig
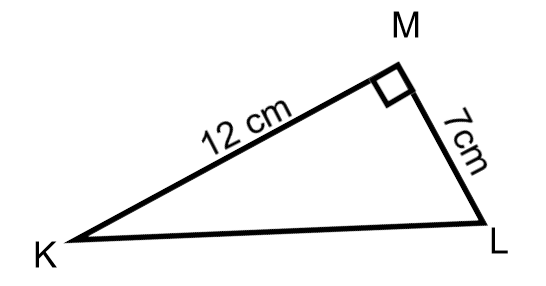
KL is schuine zijde
KL² = 7² + 12² = 49 + 144 =193
KL = sqrt193=13,89..
KL=13,9 cm
200
Bereken de zijde met een ?, rond af op 1 decimaal.
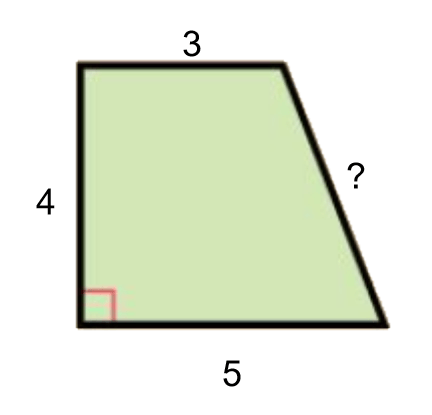
2² +4² = 4 + 16 = 20
sqrt20 = 4,47..dus
?=4,5
300
Schrijf de stelling van Pythagoras op.
rechthoekszijde² + rechthoekszijde² = schuine zijde²
300
Bereken de afstand tussen A(7, -2) en B(-1, 4) op 1 decimaal nauwkeurig
x verschil is 8
y verschil is 6
AB² = 8² + 6² = 64 +36 = 100
AB = sqrt100= 10
300
Het dak is symmetrisch.
Bereken de hoogte van het bovenste deel van het dak op (dus gebruik de 2,6 en de 1,5) rond je antwoord af op 2 decimalen
hulplijn zodat je een driehoek krijgt met zijde 1,3 m en schuine zijde van 1,5 m
hoogte² = 1,5²-1,3² = 2,25-1,69=0,56
hoogte = sqrt0,56 = 0,748..
dus hoogte = 0,75m
400
Schrijf de stelling van Pythagoras bij de driehoek hieronder op.
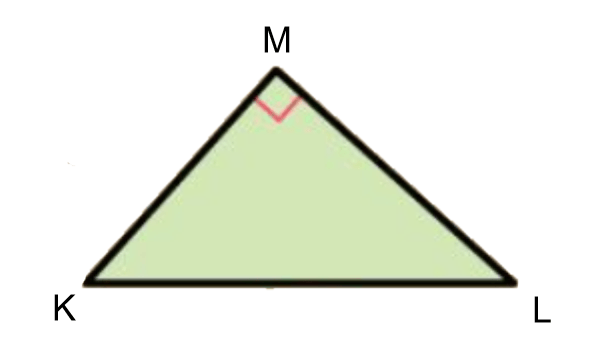
KM² + LM² = KL²
400
in driehoek EFG is hoek F 90o
EF = 5 cm
EG = 10 cm
Bereken FG op 1 decimaal nauwkeurig.
FG is een rechthoekszijde
dus FG² = 10² - 5² = 100 - 25 = 75
FG = sqrt75 = 8,66..
FG = 8,7cm
400
Bereken de totale hoogte van het huis. Rond af op 2 decimalen. De afmetingen zijn in meter.
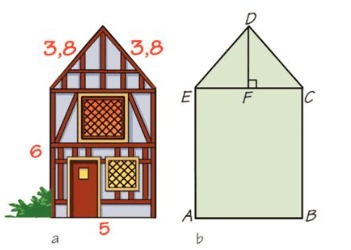
DF² = 3,8²-2,5² = 8,19
DF= sqrt8,19 = 2,861..
DF = 2,86 m
totale hoogte = 2,86+6=8,86m
500
Wat is een ander woord voor de schuine zijde?
hypotenusa
500
Is driehoek ABC rechthoekig?
Leg je antwoord uit met een berekening
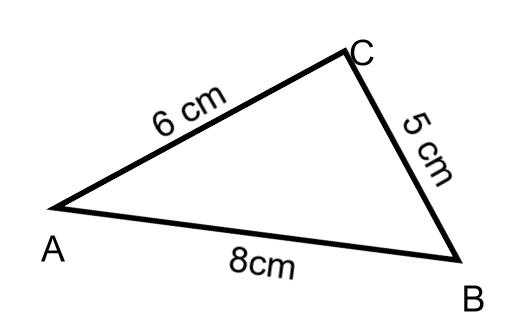
5² +6² = 8² ?
25 +36 = 61 8² =64
dus nee is niet rechthoekig
500
Bereken QT op 1 decimaal nauwkeurig.
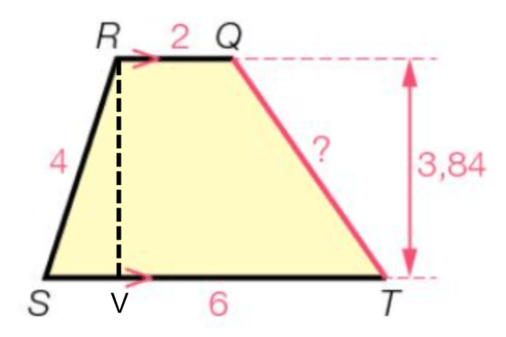
eerst SV bereken
4²-3,84² = 1,2544
SV = sqrt 1,2544
vanuit Q een hulplijn naar beneden noem even W. Vanuit dat punt naar VW = 2.
WT = 6-2-sqrt1,2544