Mixed Review 1
Mixed Review 2
Mixed Review 3
Mixed Review 4
Mixed Review 5
100
What types of transformations are occuring?
-4f(x+5)
Horizontal shift left 5
Reflection over the x-axis
Vertical Stretch by a factor of 4
100
Find the area of the following triangle. Round to the nearest hundredth.
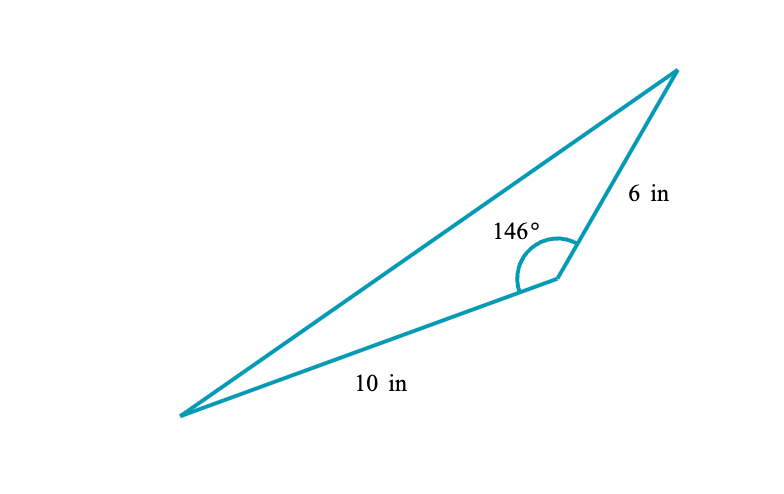
16.78 in2
100
Write the equation given the x-intercepts are 3 & 5 with a vertex of (4, 3).
y = -3(x-3)(x-5) or y = -3x2 + 24x - 45
100
Find a possible value of x so that 4 < log x < 5.
NO calculator
x can be any number between 10,000 and 100,000
100
Find the altitude of an equilateral triangle if the side lengths are 20 units.
10sqrt3 units
200
Find the missing side lengths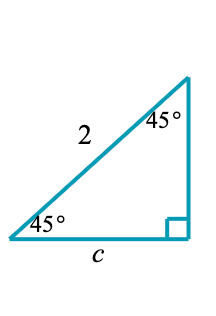
sqrt2 for both legs
200
Solve the following: 6x2 - 4x = 2 +3x
x = (7+-sqrt97)/12
200
Solve: 9(103x+2)=90,000
x = 2/3
200
Mountain officials want to build a new ski lift from B to C, as shown in the figure below. The distance from A to C is 1520 feet. They measure angle DAC to be 38° and angle DBC to be 25°. What is the distance from A to B? Round your answer to the nearest tenth of a foot.
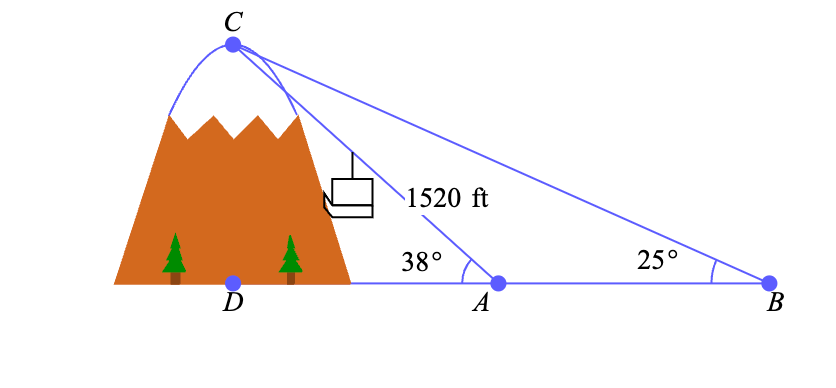
809.1 ft
200
What is the area of a square with a diagonal length of 24 units.
Area = 288 units2
300
Factor 5x2 + 15x - 50
5(x+5)(x-2)
300
Given f(x) = 2x2 - x, write the equation g(x) when the following transformations occur. Write in terms of x.
Horizontal translation 5 right
Vertical translation 3 down
g(x) = 2(x - 5)2 - (x - 5) - 3
300
Find the angle of depression from the top of a lighthouse that is 200 ft above water level to the waterline of a ship 1191 ft offshore. Round your answer to the nearest tenth of a degree.
9.5 degrees
300
Keiko wants to know the length of a tunnel built through a mountain. To do so, she makes the measurements shown in the figure below. Use these measurements to find the length of the tunnel. Round to the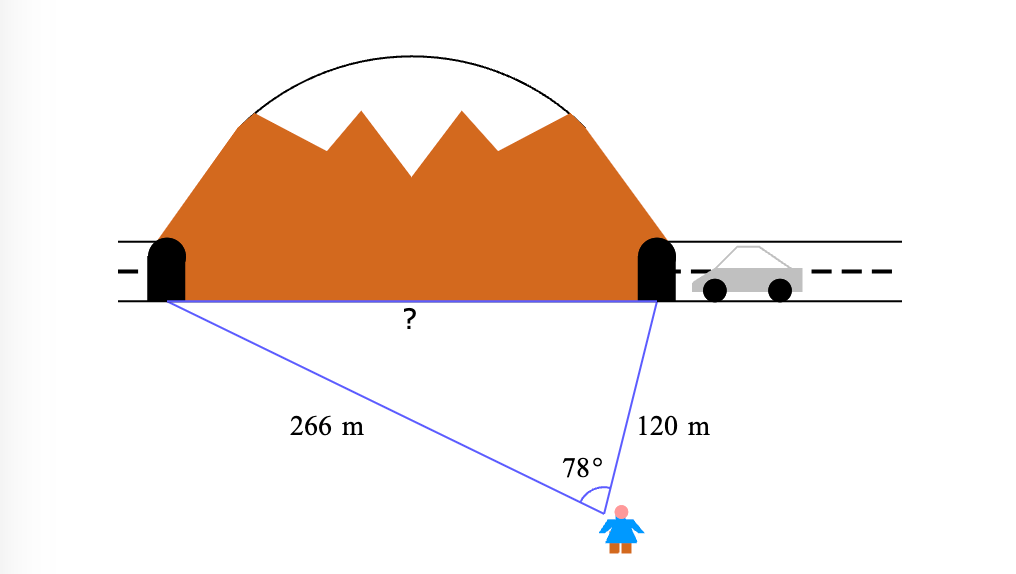 
nearest hundredth.
268.11 m
300
10log x is equal to _______
x
400
You are looking up at the school building and wondering how tall it really is. You sight the top of it standing on the ground with an angle of elevation of 53 degrees. You are 47.3 meters from the base of the front of the building. How tall is the building if you are 1.75 meters tall?
The total height of the building is about 64.52 meters
400
Solve 4x2 + 7x = 15
x = 5/4 or x = -3
400
Solve 806 = 8(102x-1) + 6
x = 3/2
400
Write a quadratic equation in standard form if the x-intercept is 4 and the y-intercept is 8.
y = 1/2 x^2 -4x + 8
400
Factor 4x3 - 22x2 - 12x
2x(2x +1)(x - 6)