inductive
Identify the hypothesis and conclusion of the following conditional:
If you do not pray, then you will not be saved.
Hypothesis: you do not pray
Conclusion: you will not be saved
The law that tells us: given "if p, then q" and "p", we can conclude "q" is called the:
Law of Detachment
The property that tells us we can switch what is on each side of an equation is called the:
Symmetric Property of Equality
If p is true and q is true, what is the truth value of:
~p v q
true
The three ways we talked about solving a system of equations are:
1. Elimination
2. Substitution
3. Graphing
True or false. If false, give a counterexample.
If a shape is a quadrilateral, then it is a square or rectangle.
Trapezoid
V is the symbol for a statement with the word ____.
⋀ is the symbol for a statement with the word ____.
OR, AND
The law that tells us if we are given "if p then q" and "if q then r", we can conclude "if p then r" is called the:
Law of Syllogism
Suppose we had these steps:
Step 5: 4 + 5x + 8 = 2x - 8 + 8
Step 6: 12 + 5x = 2x
What is the reason for step 6?
Substitution
What are the solutions to this system?
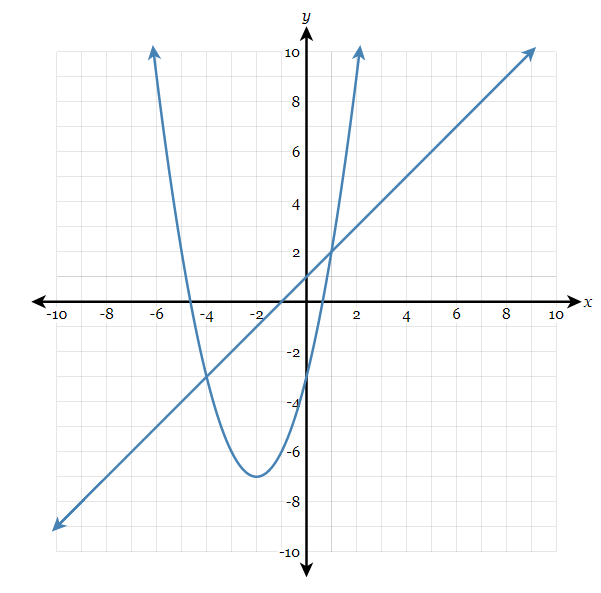
(1,2) and (-4,-3)
A system of equations is defined as a group of how many equations?
Two or more
True or False? If false, give a counterexample.
If x^2 =25, then x = 5.
False. Counterexample: x = -5
Write the contrapositive of the following conditional:
If you are not living, then you are dead.
If you are not dead, then you are living.
Make a valid conclusion using the law of detachment or the law of syllogism, if possible. If not, say "no valid conclusion" and explain.
If tomorrow is Friday, then today is Thursday.
If today is Thursday then yesterday was Wednesday
Valid Conclusion: If tomorrow is Friday, then yesterday was Wednesday.
Substitution
An OR statement is called a ____________.
An AND statement is called a _____________.
disjunction, conjunction
Find y:
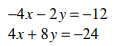
y=-6
Make a conjecture about the pattern and find the next term in the sequence.
Example: These are the perfect squares; the next term is 25.
p: I get a job
q: I will earn money
r: I will spend money
Tell me in words; what is ∼p→~q?
If I do not get a job, then I will not earn money.
State the Law of Detachment.
If "if p then q" is true and "p" is true, then "q" is true.
(If given "if p then q" and "p", we can conclude "q", assuming "if p then q" and "p" are true")
When do we use the reflexive property?
We use the reflexive property because we need to show that what we are about to add/subtract/multiply/divide (on both sides of the equation) is actually the same thing.
Suppose that a conditional was written as w→ z.
Tell me in words what the symbols would be for the following...
converse
inverse
contrapositive
converse: z → w
inverse: ~w→ ~z
contrapositive: ~z→ ~w
Find y.
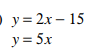
y=-25
Make a conjecture about the sum of three prime numbers. Give three examples to back up your claim.
The sum of three prime numbers is an odd number.
Examples:
3+3+3=9
5+5+5=15
7+3+5=15
Suppose that a conditional was written as w→ z.
Tell me in words what the symbols would be for the following...
converse
inverse
contrapositive
converse: z → w
inverse: ~w→ ~z
contrapositive: ~z→ ~w
The law of logic "Modus Tollens" tells us if we are given "if p then q" and "~q", we can conclude "~p".
Given: If water reaches a temperature of 0 degrees Celsius, then it will freeze.
Water will not freeze.
What is a valid conclusion?
Water does NOT reach a temperature of 0 degrees Celsius.
Write the following proof on your paper. Then share your screen for the answer.
Given:5(x+1) = 30
Prove: x = 5
5(x+1)=30 (Given)
5x+5=30 (Distributive Property)
5=5 (Reflexive POE)
5x+5-5=30-5 (Subtraction POE)
5x=25 (Substitution)
5=5 (Reflexive POE)
5x/5=25/5 (Division POE)
x=5 (Substitution)
Give ALL the counterexamples for the following statement:
"If x > 0, then x > 1."
Any number between 0 and 1, including 1.
Find the solution to the system.
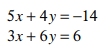
(-6,4)