root(m)(root(n)(x))=
root(m)root(n)(x)
What is the end behavior of the given function?
y=-x^6+x^2-100
x-> infty, y -> -infty
x -> -infty, y -> -infty
logA^c=
clogA
True or False, if it's false, please give an example.
The horizontal asymptote when m > n is
a_m/b_n
for
y=(a_mx^m+a_0)/(b_nx^n+b_0
No horizontal asymptote.
y=(2x^2-1)/(x+1)

The given expression approaches to ________ when
x->infty
(1+1/x)^x
e
Simplify the given expression.
(a^2)^-3(a^3b)^2(b^3)^4
b^14
What is the axis of the symmetry of
y=2x^2-3x-1
x=3/4
Evaluate the logarithmic expression.
log_8 6-log_8 3+log_8 2=
x=2/3
Find the horizontal asymptote of
1/(x^2+1)
Evaluate the given expression
4^(3log_2 ((3x)/2)
(27x^3)/8
Graph. State its asymptote.
y=-2^(x-1)+3
Horizontal Asymptote: y = 3
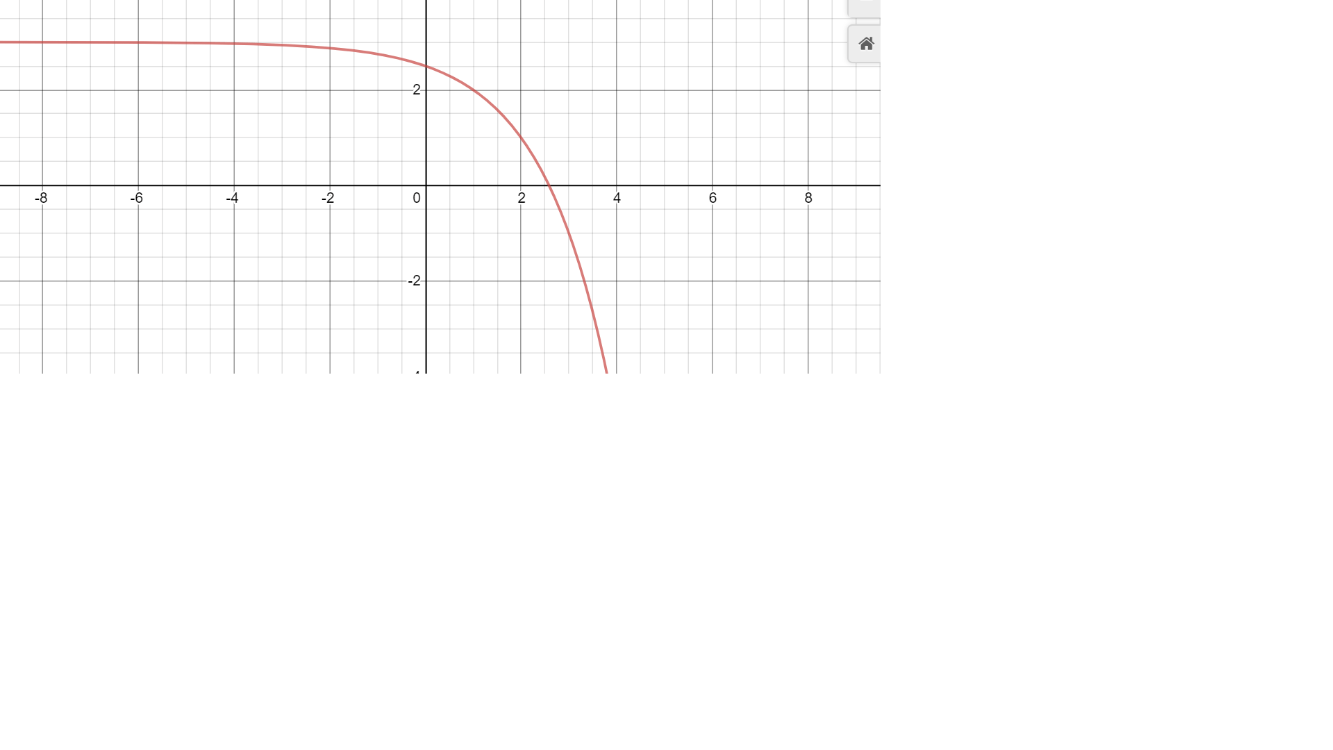
Graph. State its domain and asymptotes if there are any.
root(3)(x+1)-5
Domain: x is all real numbers. No asymptotes. 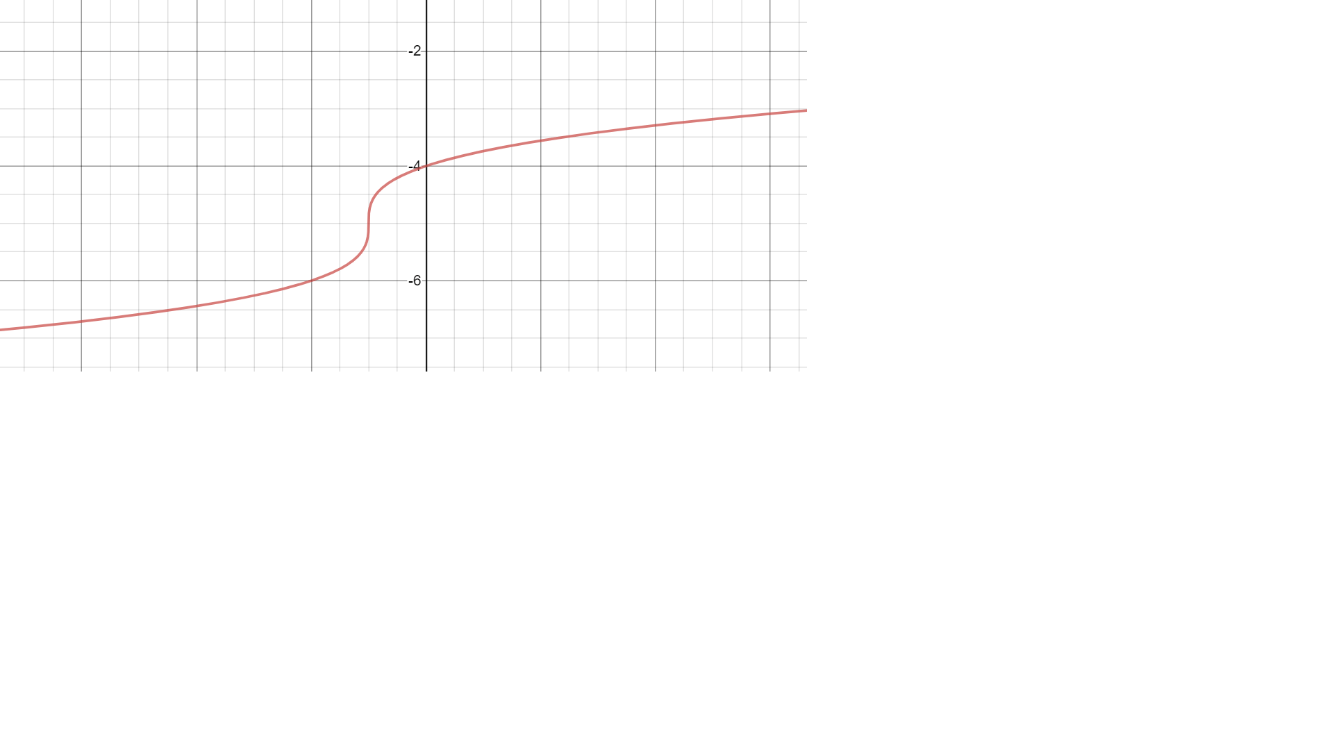
Are given two functions the same?
Please find the domains for each function.
y=lnx^2
y=2lnx
No.
The domain for
y=lnx^2
is
x!=0
For the other function, the domain is x > 0.
Graph and state its asymptotes
y=-1/x
Vertical Asymptote: x = 0
Horizontal Asymptote: y = 0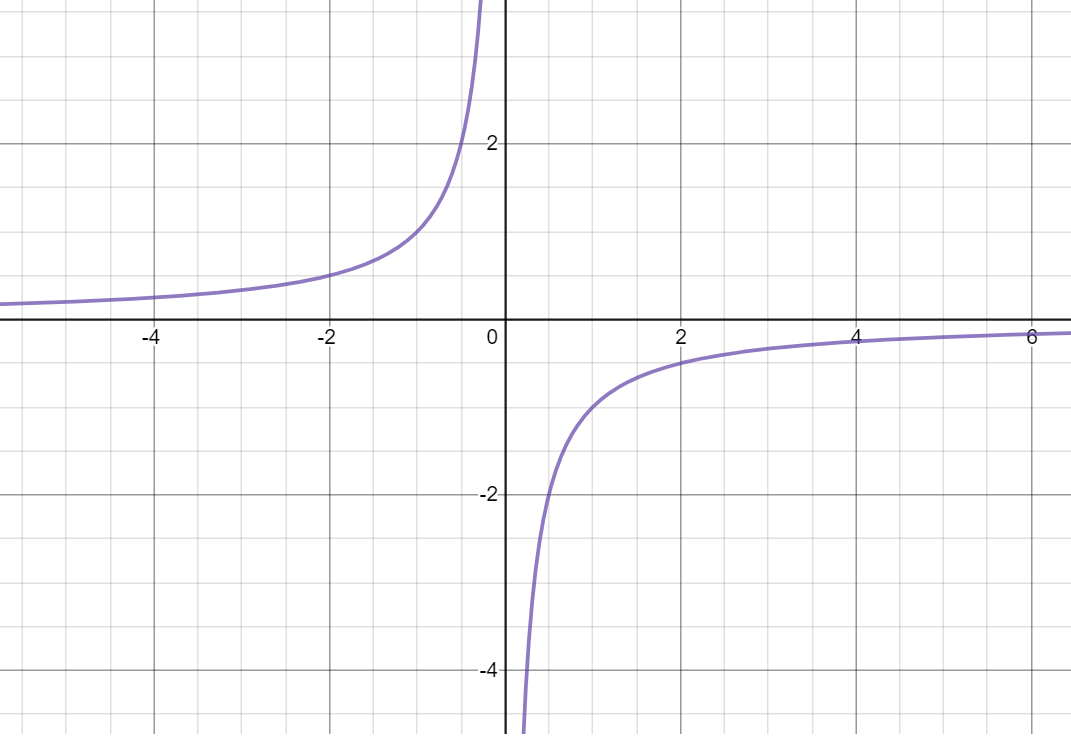
Given a point (2, 5), please write down a line equation that is perpendicular to y-axis and passes through (2, 5)
y = 5
Akito is a great kid who is respectful and loves to save money. He got a reward from IBSC as the best helper. He received $1000. Instead of spending it all, he wants to deposit all $1000 in the Bank of Spiderman which earns 5% interest semiannually. How much interest may Akito earn in two years? (Set up the equation only)
1000(1+0.05/2)^4
What is the range of
y=x^2-x
y>= -1/4
What is the domain of
y=log(2x+1)-5
x > -1/2
What is the range of
y=(1-x)/(5x-1)
y!=-1/2
What is the domain of
y=1/sqrt(x+1)
x > -1
Find the domain of
y=10^(x^2)+log (1-2x)
x>1/2
Solve
y=6e^(4x)+e^(2x)-1
x=1/2 ln(1/3)
Solve
log_8 (x+5) - log_8 (x-2) = 1
x=3
Simplify the given expression.
((x-1)(x^3 + 27))/((x+3)(x^2-1))
(x^2+3x+9)/(x+1)
Given a graph of f(x),
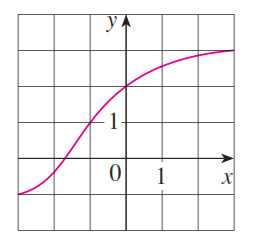 Find
Find
f^-1 (2)=
f^-1(2)=0