Theorems and Postulates
Rules for Triangle Sides
Points of Concurrency
Perpendicular Bisectors
Solving for the Unknown
100
Which of the following are vertical angles?
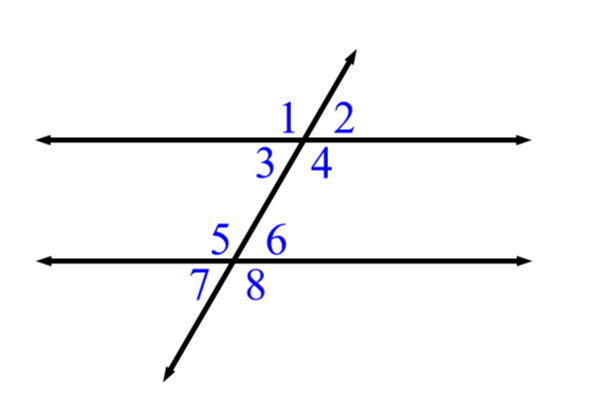
1 and 4
2 and 3
5 and 8
6 and 7
100
Which of the following side lengths listed can create a triangle?
2, 3, 7 19, 23, 40
8, 4, 11 35, 25, 60
19, 23, 40
8, 4, 11
100
Find the centroid of the triangle with the given endpoints:
(A) (-3, 7), B(9, -1), and C(4, -9)
(3 1/3, -1)
100
Find QS.
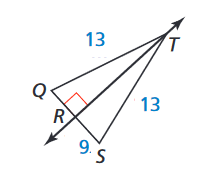
18
100
N is the incenter of △ABC. ND = 6x - 1, NE = 4x +7. Find NF.
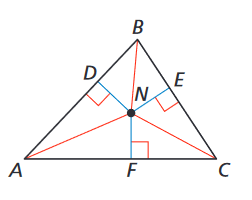
23
200
Name a pair of Corresponding Angles.
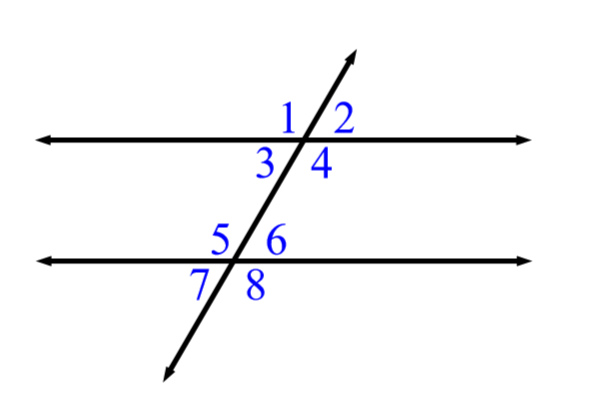
1 and 5
2 and 6
3 and 7
4 and 8
200
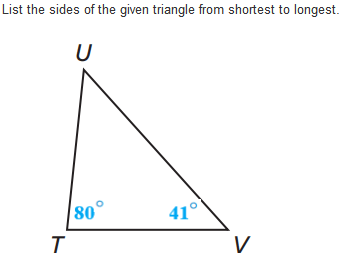
UT, TV, UV
200
Find the coordinates of the circumcenter of △ABC with vertices A(0, 3), B(0, −1), and C(6, −1).
(3, 1)
200
Find UW.
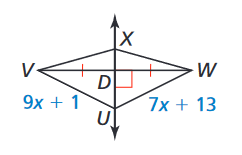
55
200
When AB = 5x + 1 and GJ = 6x + 18. What is GJ?
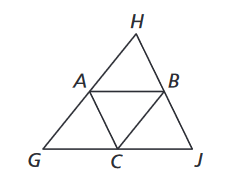
42
300
300
Two lengths of a triangle measure 3 feet and 27 inches. Below there are several measures for the third side of the triangle. Determine which of the lengths shown below can create a triangle with the 2 sides.
(a) 7 inches (b) 5 ft 3 inches
(c) 4 feet 5 inches (d) 1 foot 1 inch
(c) and (d)
300
Find the coordinates of the orthocenter of △XYZ with vertices X(−5, −1), Y(−2, 4), and Z(3, −1).
(-2, 2)
300
Write an equation of the perpendicular bisector of the segment with the endpoints P(-4, 7) and Q(6, -1).
y=5/4x+1 3/4
300
Point D is the centroid of △ABC. Use the given information to find the value of x.
BD = 7x - 8, BF = 9x + 6
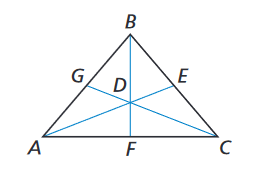
x = 12