Unit 1A: Constructions
Unit 1B: Rigid Transformations
Unit 2: Congruence
Unit 3: Similarity
Potpourri
100
Line XY is the ________________ of segment PQ.
Perpendicular Bisector
100
Triangle A'B'C' is the image of triangle ABC after a _____________.
Translation
100
What does congruent mean (informally)?
The same; one fits exactly on top of the other; etc.
100
What does similar mean? (informally)
Same angles, different size. One thing can be dilated to be congruent, or the exact same, to another.
100
This US State is home to Acadia National Park.
Maine
200
Ray OC is the __________________ of angle BOA.
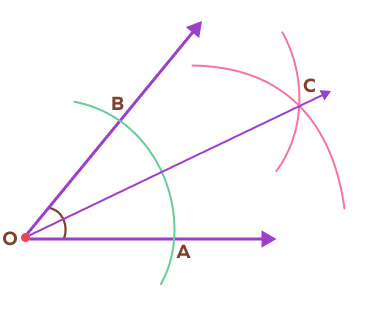
Angle Bisector
200
Triangle A'B'C' is the image of triangle ABC after a ______________ over __________.
reflection, y-axis
200
This is our definition of congruent (formally).
There is a sequence of rigid motions that takes one figure exactly onto another, such that all points coincide.
200
This is our definition of similar (formally).
There is a sequence of rigid motions and dilations that takes one figure exactly on to the other, such that all points coincide.
200
This type of tree produces acorns.
Oak
300
This is our definition of a perpendicular bisector.
The set of all points equidistant from two endpoints of a segment.
300
Triangle A'B'C' is the image of triangle ABC after a ____________ of _________ degrees ____________(direction) around point ____.
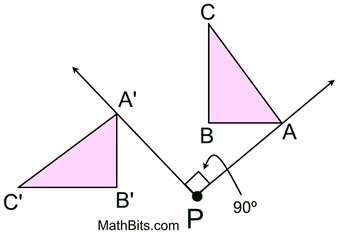
Rotation, 90, clockwise, P
300
These are the three triangle congruence theorems.
Side-Angle-Side (SAS)
Angle-Side-Angle (ASA)
Side-Side-Side (SSS)
300
Are these two triangles similar, why or why not?
Yes, angle angle triangle similarity.
300
This actor played 'Ken' in the Barbie Movie.
Ryan Gosling
400
Explain how you know quadrilateral ABDC is a rhombus (all sides equal length).
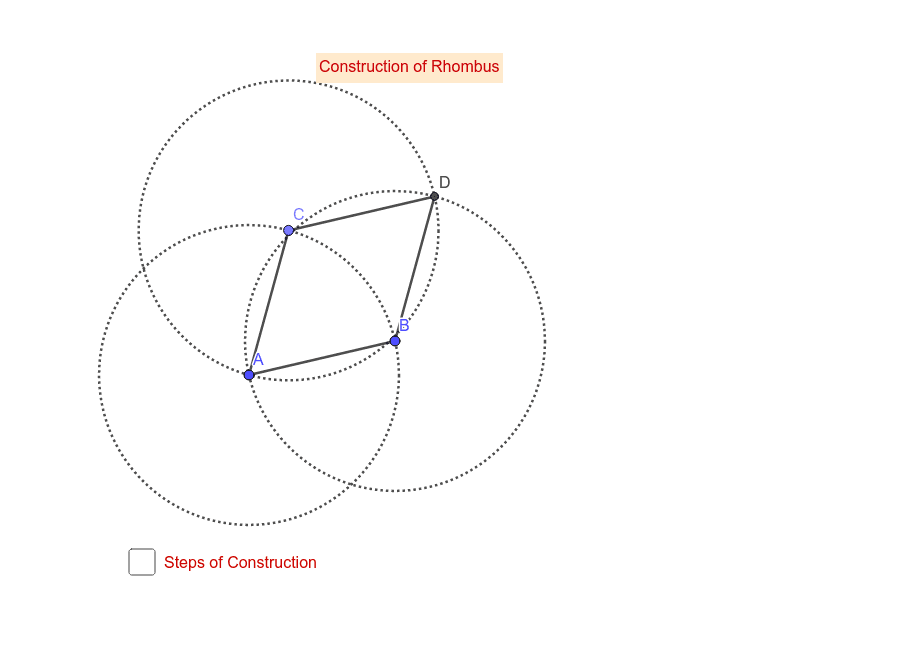
Each side of the quadrilateral is a radius of a congruent circles. We know the circles centered at C, B, and A are congruent because they pass through each others centers, so each radius is the same length.
400
Write a sequence of rigid motions that takes triangle ABC onto triangle A'B'C'.
Answers vary.
400
Explain how you know triangle EAD is congruent to triangle ECB.
Angle A is congruent to angle C, angle DEA is congruent to angle BEA, and EA is congruent to EC, therefore, the two triangles are congruent by the Angle Side Angle Triangle Congruence Theorem.
400
Describe a sequence of rigid motions and dilations to take triangle ABC to triangle PQR, and write a similarity statement.
Answers vary.
400
This Ancient Greek philosopher wrote a book titled Republic, primarily exploring 'justice' as it relates to states and individuals.
Plato
500
How would you construct the line of reflection to take a point A to another point, B?
Construct the perpendicular bisector of segment AB.
500
In the diagram below DA is congruent to BA and DC is congruent to BC. Explain how you know a reflection across line l will take point D to point B.
Points A and C are on the perpendicular bisector of DB, since A is equidistant to D and B, and since C is equidistant to D and B. Therefore, line l the line of reflection that will take point D to point B.
500
Imagine drawing diagonal WY in the figure below to create two triangles. Write a congruence statement, and prove they are congruent.
Triangle WYX is congruent to triangle WYZ because side WX is congruent to side WZ, side XY is congruent to side ZY, and side WY is congruent to itself. Therefore, the two triangles are congruent using side side side triangle congruence theorem.
500
Identify the scale factor to take triangle ABC to triangle PQR.
PQ/AB
PR/AC
QR/BC
500
This tree species, found in the deserts of the southwest US, is nearly extinct because of its reliance on (the now extinct) giant sloths to transport its seeds.
Joshua Tree (Yucca Brevifolia)