Antiderivatives
Riemann Sum & Area
Integrals
u-Substitution
Fundamental Theorem
100
f'(x)=3x^2
f(x)=x^3+C
100
The width of each rectangle when you divide the interval
[a,b]
into n rectangles.
(b-a)/n
100
int_0^1 3x^2+1 dx
2
100
int (3x+1)^4 dx
1/15 (3x+1)^5+C
100
Find the error:
int_a^b f(x)dx = F(a)+F(b)
int_a^b f(x)dx = F(b)-F(a)
200
f'(x)=sin(x)
f(x)=-cos(x)+C
200
The area under the curve: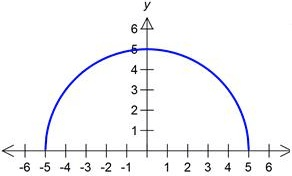
25/2 pi
200
int sec(x)tan(x) dx
tan(x)+C
200
int 1/(2x+3)dx
1/2 ln|2x+3|+C
200
Determine f(5) if f(2)=1 and
int_2^5 3f'(x)dx = 12.
f(5)=5
300
f'(x)=x^3 and f'(1)=1
f(x)=1/4 x^4+3/4
300
sum_(j=1)^n k
(n(n+1))/2
300
int 5/x dx
5ln|x|+C
300
int 2 e^(3x)dx
2/3 e^(3x)+C
300
d/dx int_1^x sin(t^3)dt
sin(x^3)
400
f'(x)=3sec(x)tan(x)
f(x)=3sec(x) + C
400
Find area from 0 to 3 under the curve:
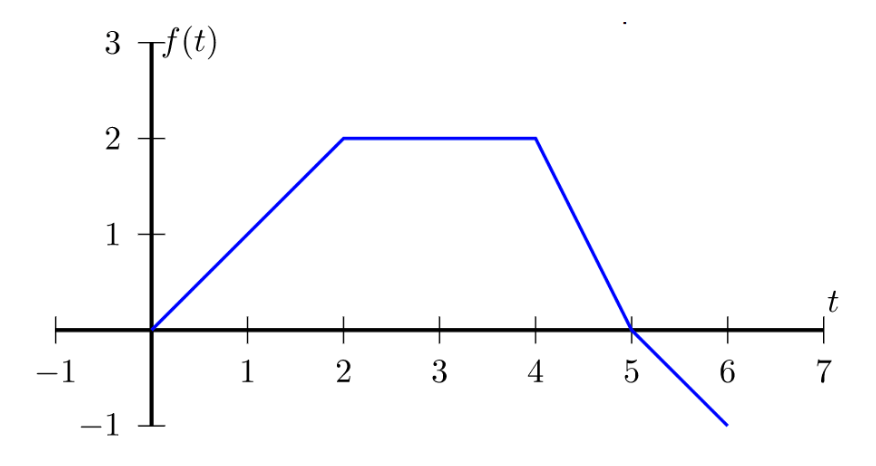
4
400
int sqrt(x) dx
2/3 x^(3/2) + C
400
int x(x+1)^5dx
1/7 (x+1)^7 - 1/6 (x+1)^6 +C
400
d/dx int_3^(x^2) sqrt(t-1) dt
2x sqrt(x^2-1)
500
f'(x)=1/(x^2+1)
f(x)=arctan(x)+C
500
The below limit represents what area?
lim_(n->oo) 4/n sum_(k=1)^n sqrt(2+4/n k)
int_2^6 sqrt(x) dx
500
int (4e^x+e) dx
4e^x+ex+C
500
int sin^2(x)cos(x)dx
1/3 sin^3(x)+C
500
d/dx int_(2x)^(3x) tan(t)dt
3tan(3x)-2tan(2x)