Unit 2: Evaluating Logarithms
Unit 2: Graphs
Unit 2: Exponents and Logarithm rules
Unit 1: Linear, Exponential, Quadratic
Unit 1: Writing Inverse Functions
100
What is log416?
Answer: 2
Because 42 = 16
100
What is the y-intercept of this graph?
Answer: (0, 4)
100
Simplify
(x^2y^4)/y^2
Answer: x2y2
100
Which type of function (linear, quadratic, exponential) has a constant difference between each consecutive y-value?
Answer: Linear functions
100
Write the inverse equation for f(x) = 3x .
Answer: f-1(x) = log3x
The inverse of an exponential function is log to the same base.
200
What is log2(1/8)?
Answer: -3
Because 2-3 = 1/8 and 1/23 = 1/8
200
What is the equation for this line?
Answer: y = -3/4x + 4
The slope is -3/4 and the y-intercept is 4.
200
Rewrite log2(x2) using the appropriate rule.
Answer: 2 log2 x
Use the power rule.
200
Which type of function (linear, quadratic, or exponential) has no x-intercept?
Answer: Exponential
The y-values will never reach 0!
200
Write the inverse equation for
f(x)=3x-2
Answer:
f^-1(x)=(x+2)/3
300
What is log77x?
Answer: x
Because 7x = 7x
300
What is the x-intercept of this graph?
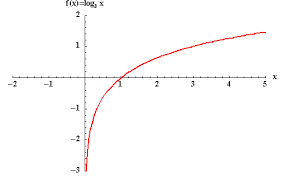
Answer: (1, 0)
300
Simplify using no negative exponents
(x^2y)/(x^3y^2)
Answer:
1/(xy)
300
Which type of function (linear, quadratic, or exponential) can have two x-intercepts?
Answer: Quadratic
Quadratic functions form a parabola and can cross the x-axis twice (but some don't ever cross and some touch only at the vertex).
300
Write the inverse function for
f(x)=2x^2
Answer:
f^-1(x)=sqrt(x/2)
400
Rewrite log2(x) = 10 in exponential form.
Answer: 210= x
The power in the exponential form is the answer of the logarithm.
Here x = 1024
400
What is the y-intercept of this graph?
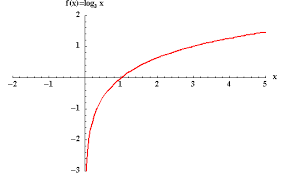
Answer: There is no y-intercept!
Unless a log function has been translated left, there is an asymptote at x = 0 for all these functions.
400
Expand log(x2y).
Answer: 2 log x + log y
Use the product rule: log (x2) + log y
Then use the power rule: 2 log x + log y
400
A linear function starts at 2 and adds 2 each time.
An exponential function starts at 1 and multiplies by 2 each time.
Write the first 3 terms of each function.
Answer: Linear - 2, 4, 6 Exponential - 1, 2, 4
400
What is the inverse function for
f(x)=(x+1)^3
Answer:
f^-1(x)=root(3)x-1
500
Rewrite 10x = 400 in logarithmic form.
Answer: log10 400 = x or log 400 = x
The answer to a log is the exponent attached to the base.
Here x = 2.602
500
The parent graph (dashed) is y = log x. What is the equation of the "child"?
Answer: y = 4 + log(x-5)
The marked point shifts 4 up and 5 to the right.
500
Given log45 = 1.2 and log43 = 0.8
Find log427. Show your process.
Answer: 2.4
log427 = log4(3*3*3) = log4(3)+log4(3)+log4(3) = 0.8+0.8+0.8 = 2.4
500
A linear function starts at 2 and adds 2 each time.
An exponential function starts at 1 and multiplies by 2 each time.
After how many terms will the exponential function be larger than the linear function?
Answer: 5 terms
Linear - 2, 4, 6, 8, 10
Exponential - 1, 2, 4, 8, 16
500
What is the inverse function for f(x) = 3(10x)
Answer: f-1(x) = log3(x/3)
First undo multiplication, then undo the power with the log.