Definitions
Graph Features
Adjacency Matrices
Miscellaneous Graphs and Networks
Walks
100
An edge
What is the name of the line that connects two vertices?
100
What is the degree of vertex C?
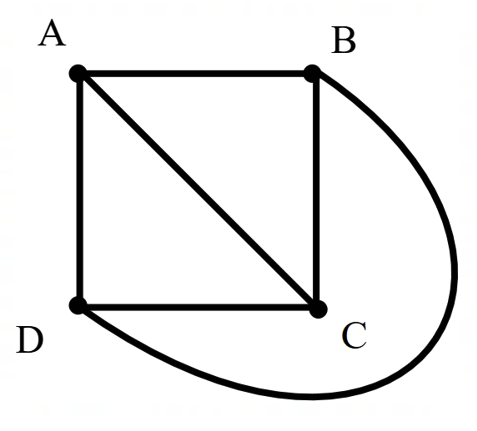
deg(C)=3
100
An adjacency matrix is always a ______________ matrix.
square
100
When two vertices are joined by more than one edge
What are multiple edges?
100
What type of walk cannot revisit the same edge and end at any vertex?
A Trail
200
An edge that joins a vertex to itself
What is a loop?
200
What is the degree of an isolated vertex?
0
200
How do we recognise a loop on a vertex from an adjacency matrix?
A 1 in the lead diagonal for that vertex
200
What is an odd vertex?
A vertex that has a degree that is an odd number.
200
What is a Hamiltonian Path?
A walk that goes through every vertex only once.
300
A graph where every vertex is connected to any other vertex, directly or indirectly
What is a connected graph?
300
How many faces in this graph?
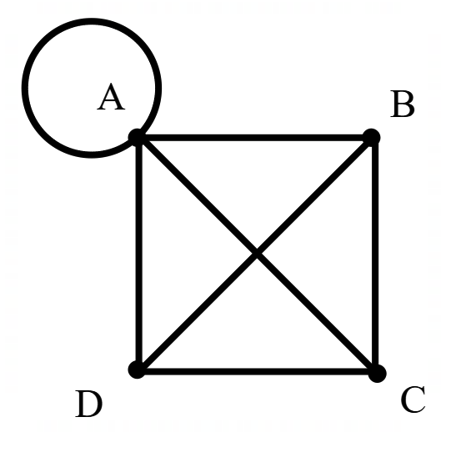
5. Remember to make it a planar graph before you count the faces.
300
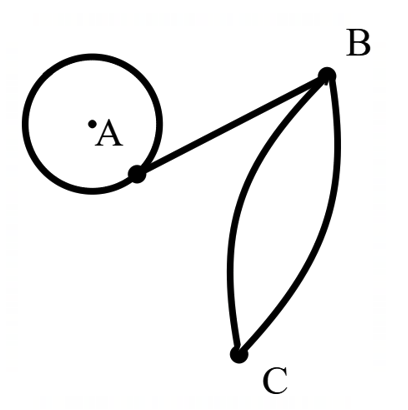
Create the adjacency matrix for this graph.
300
Graphs that contain identical information
What are isomorphic graphs?
300
How many edges would be required to create a Hamiltonian Cycle with 300 Vertices.
300
400
What distinguishes a Planar graph from other graphs?
A planar graph has no crossed edges.
400
An edge that, if removed, leaves the graph disconnected.
What is a bridge?
400
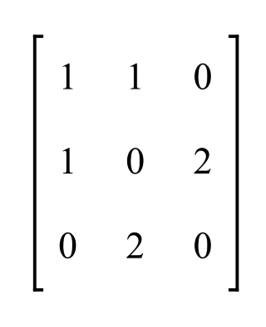
What type of graph does this adjacency matrix represent.
A complete graph with four vertices
400
What is the sum of degrees?
The number of vertices is equal to twice the number of edges.
400
PowerPoint Slide Question 1
Hamiltonian Cycle
500
A graph where all vertices connect directly to every other vertex
What is a complete graph?
500
Name one industry where connectedness of a network is critical.
Airline
Communication systems
Computer networks
500
A graph with 7 edges and 5 faces will generate
a ______ x ______ adjacency matrix.
4 x 4. Use Euler's formula to calculate the number of vertices.
v = e - f + 2
500
f=e-v+2
Euler's formula rearranged to find the number of faces in a planar graph
500
Why is a degree sum of 15 impossible?
Degree sum is 2 x number of edges