Rules
Notation
2x4, when x=-3
162
x^2 x^3
x^5
(x^6 y z^-2)^5
Write the answer using positive exponents
(x^30 y^5)/(z^10)
Write 6800000 in scientific notation
6.8 x 106
Is the table linear or exponential? Explain your reasoning.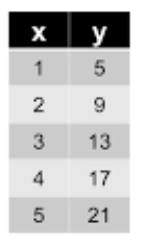
Linear. There is a common difference of 4 between the y-values.
4x2, when x=-3
36
(x^19)/(x^14)
x^5
(x^2)^11* x/x^6
x^17
Write 0.0000000063 in scientific notation
6.3 x 10-9
Is the table linear or exponential? Explain your reasoning.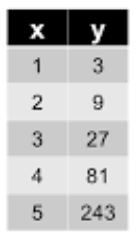
Exponential. There is a common ratio of 3 between the y-values.
3x2, when x=4
48
(x^4)^6
x^24
(x^12 y)^7
x^84 y^7
Write 6.9 x 105 in standard notation
690,000
Is this an example of a linear situation or an exponential situation? Write an equation to represent this situation. 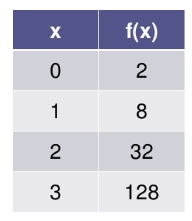
y = 2*4^x
Exponential.
5x2, when x=4
80
(x^2)/(x^2)
1
( (x^5 y)/(-2z^8) )^4
Write the answer using positive exponents
(x^20 y^4)/(16z^32)
Evaluate
((2 x 104)(6 x 105))/(3 x 107)
4 x 102
Is this an example of a linear situation or an exponential situation? Write an equation to represent this situation.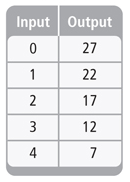
Linear.
y=-5x+27
2x2, when x=-4
32
x^2 x^-6
Write the answer using positive exponents
1/(x^4)
(x^4 y z^-7)^3
Write the answer using positive exponents
(x^12 y^3)/(z^21)
The speed of light 3 x 108 meters/second. If it takes 5 x 102 seconds for light to travel from the sun to the earth, what is the distance in meters between the sun and the earth? Express your answer in scientific notation.
1.5 x 1011 meters
The following equation represents the population (P) growth of bacteria in a petri dish after some time (t) in hours:
P=350(2)^t
What is the initial amount/value? What is the growth factor?
Initial amount/value: 350 bacteria
Growth factor: 2 (it doubles)
Evaluate -2x2y3 when x = -3 and y = -1
18
Simplify -34
81
(x^-1 (y^2 z^3)^3)/(x^-8 y^-7 z^4)
x^7 y^13 z^5
Write 4.5 x 10-7 in decimal notation
0.00000045
The following equation represents the population (P) growth of bacteria in a petri dish after some time (t) in hours:
P=350(2)^t
Based on the prediction equation, what will the bacteria population be after 1 day (24 hours)?
5,872,025,600 bacteria