Factoring
Quadratics
Quadratics
Key Features
of Quadratics
of Quadratics
Talk the Talk
Vocabulary
Vocabulary
Forms of
Quadratics
Quadratics
Double Points!!
100
Factoring is the process of changing a STANDARD form quadratic equation into _____________ form.
Intercept
100
Identify the VERTEX of the parabola.
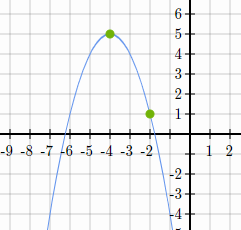
(-4,5)
100
A function whose input is squared. This means there will be two inputs that yield the same output.
The graph of this function is a parabola.
Quadratic Function
100
This form of a quadratic helps us
easily identify the Y-INTERCEPT.
Standard Form
100
EVALUATE the function for f(-3).
f(x)=x^2-2x+5
f(-3)=20
200
FACTOR the quadratic equation.
Write in INTERCEPT form.
x^2+8x+12 = 0
y=(x+2)(x+6)
200
Is this parabola concave up or concave down?
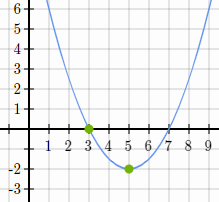
Concave Up
200
Input that produces the minimum or maximum output of a quadratic function.
Coordinate at which a parabola changes direction.
Vertex
(h,k)
200
Write the equation of the parabola in VERTEX form.
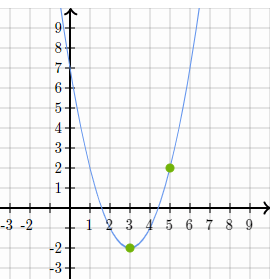
y=(x-3)^2-2
200
SOLVE for x.
5=2(x-4)^2-13
x=7 and x=1
300
FACTOR the quadratic equation.
Write in INTERCEPT form.
x^2+14x-51 = 0
y=(x+17)(x-3)
300
Find the Y-INTERCEPT of the quadratic equation.
y=3(x+5)^2-30
(0,45)
300
Roots, zeros and solutions are 3 words that mean the same as this term.
x-intercepts
300
Write the equation of the parabola in INTERCEPT form.
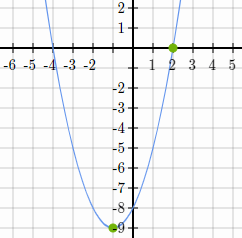
y=(x+4)(x-2)
300
FIND the STANDARD form equation for a quadratic with these X-INTERCEPTS:
x=-5 and x=3
x^2 + 2x - 15
400
Find the X-INTERCEPTS of the quadratic equation.
y=x^2+29x+28
(-1,0) and (-28,0)
400
In which QUADRANT is the VERTEX of the parabola?
y= -2(x-3)(x-7)
Quadrant 1
(5,8)
400
Parabolas that open downward. These equations have a negative leading coefficient.
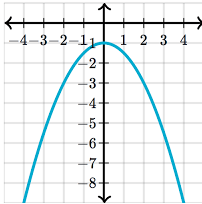
Concave Down
400
Write the equation of the quadratic in STANDARD form.
y=(x-4)(x+7)
y=x^2+3x-28
400
Find ALL the possible values of B that make the equation true.
0=x^2+Bx+15
B = -16, -8, 8, 16
500
Find the X-INTERCEPTS of the quadratic equation.
y=x^2 -13x-48
(16,0) and (-3,0)
500
Find the VERTEX of the parabola.
f(x)=x^2+4x-21
(-2,-25)
500
Numbers or expressions that are being multiplied to form a product.
Example: 2*6 or (x-3)(x+4)
Factors
500
Write the equation of the quadratic in STANDARD form.
y=-2(x+3)^2+11
y=-2x^2-12x-7
500
If the vertex of a parabola is at (-1, -4) and f(3)=12, find the other INPUT that would create this same OUTPUT...f(?)=12
f(-5)=12