En husritning är i skala 1:200. 7 cm på ritningen motsvarar så många meter i verkligheten.
Svar: 14 meter.
Vad blir blir areaskalan om du ritar av ett Pokémonkort i längdskala 4:1?
Svar: 16:1.
Hur lång är sidan som är markerad med h? Alla mått är i cm.
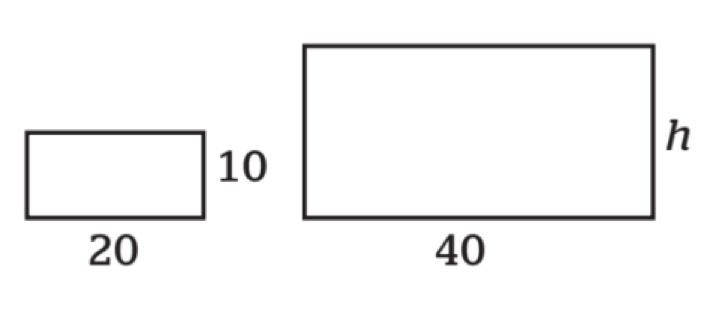
Svar: 20 cm.
I en rätvinklig triangel är den ena kateten 9 cm och den andra kateten 12 cm. Hur lång är hypotenusan?
Svar: 15 cm.
Beräkna rätblockets volym.
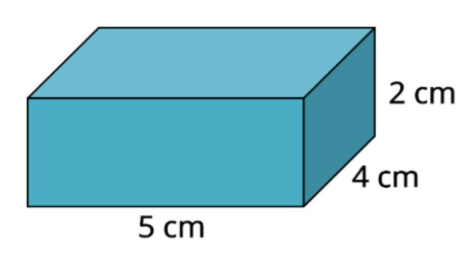
Svar: 40 cm3.
Hur stor är vinklen x?
Svar: x= 85°.
Linda är ute och orienterar. Hennes orienteringskarta har skalan 1:6 000. Mellan två kontroller är det 6,5 cm på kartan. Hur många meter är det mellan kontrollerna i verkligheten?
Svar: 390 meter.
Den lilla rektangeln har arean 7 cm2. Hur stor är den stora rektangelns area om längdskalan är 3:1?

Svar: 63 cm2.
Bestäm x, y och z.

Svar: x = 8 mm; y = 30 mm; z = 6 mm.
I en rätvinklig triangel är den ena kateten 24 cm och hypotenusan är 25 cm. Hur lång är den andra kateten?
Svar: 7 cm.
Beräkna volymen av cylindern. Svara i hela kubikmeter.
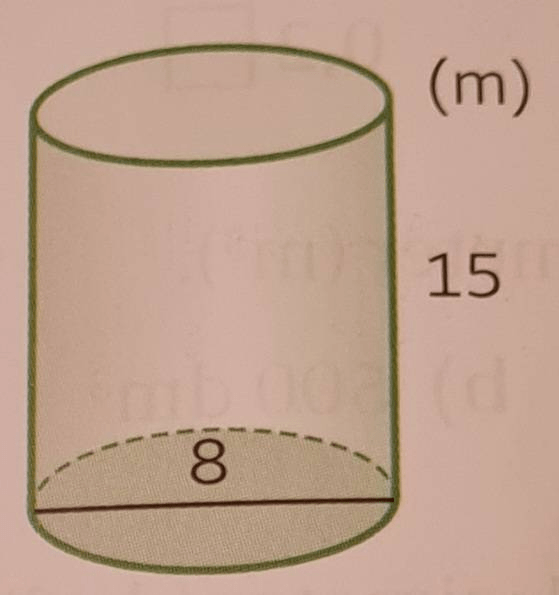
Svar: 754 m3.
Beräkna figurens area. Avrunda svaret till hela kvadratcentimeter (cm2).

Svar: 146 cm2.
En röd blodkropp är avbildad i längdskala 20 000:1. Bilden av blodkroppen är 9 cm lång. Hur lång är blodkroppen i verkligheten? Svara i millimeter.
Svar: Blodkroppen är 0,0045 mm i verkligheten.
Hur många kvadratmeter är vardagsrummet?
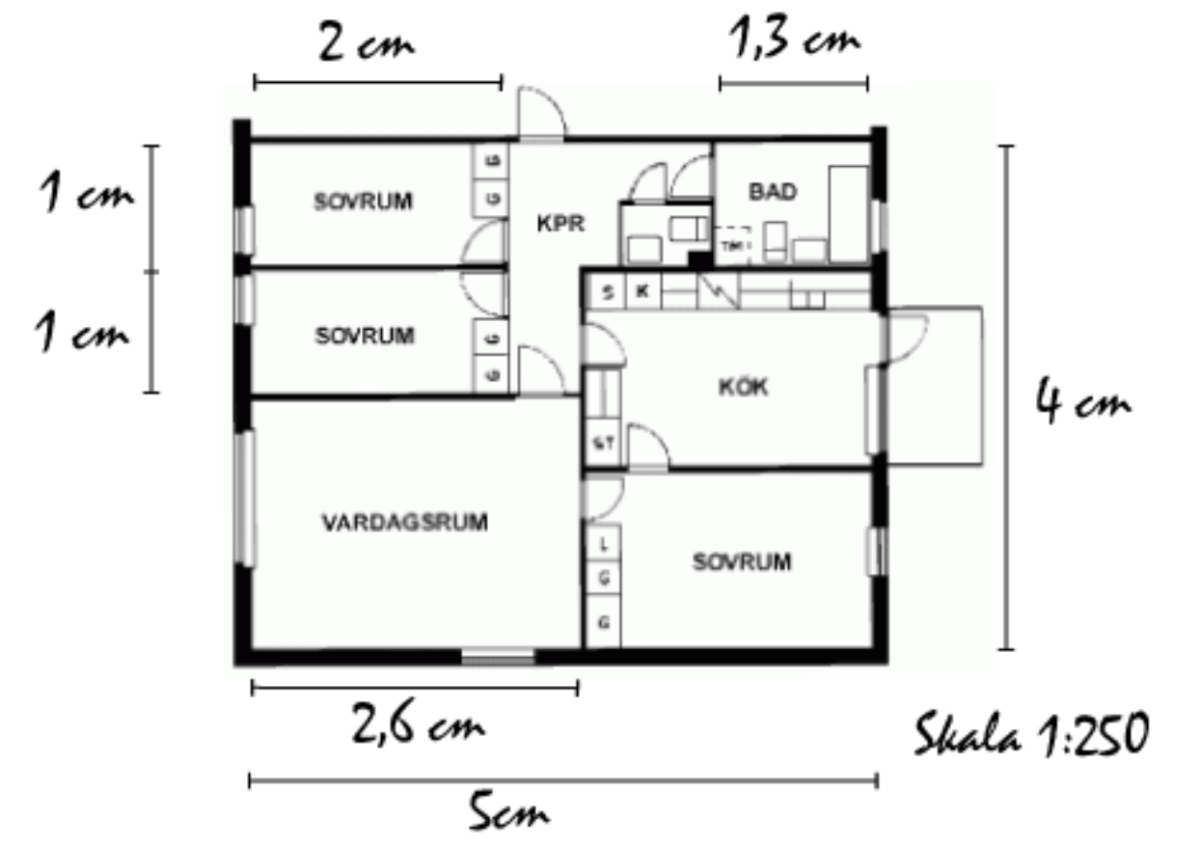
Svar: 32,5 m2.
Vilka "par av" trianglar är likformiga?
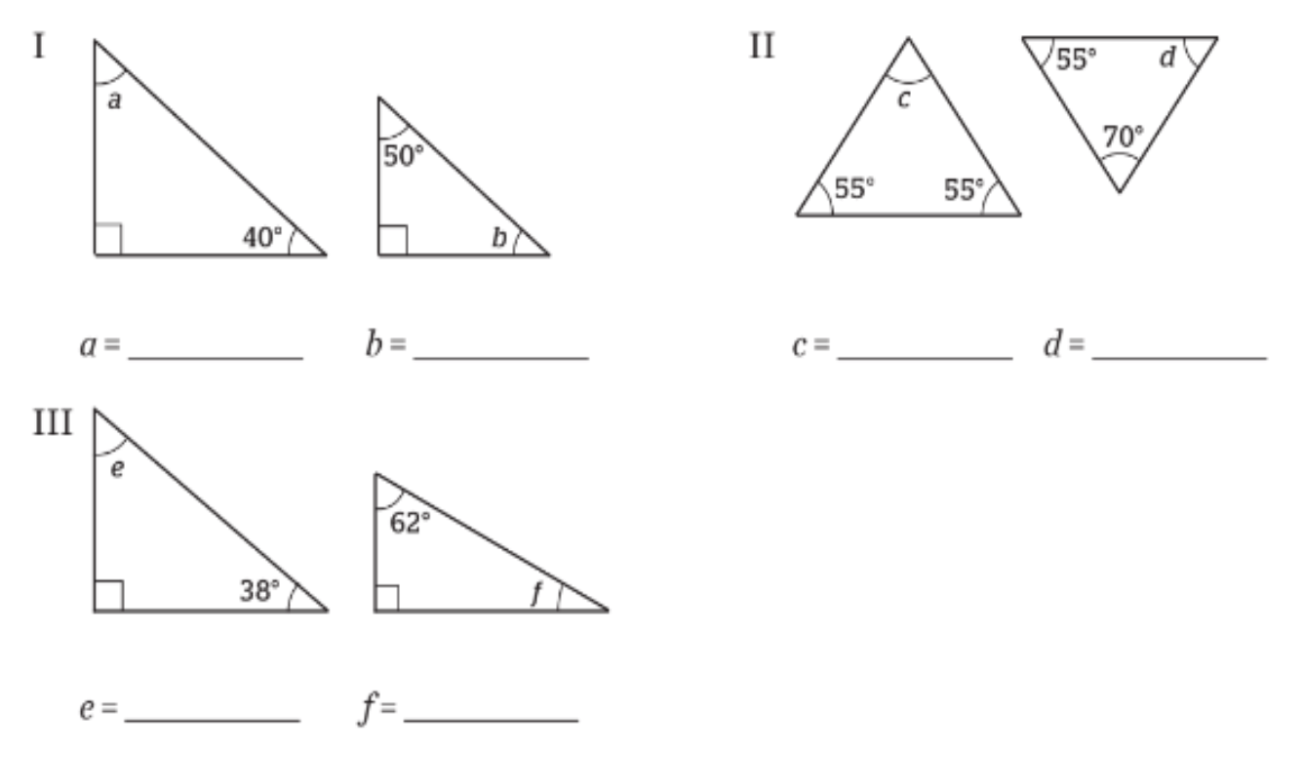
Svar: Trianglarna i I och II är likformiga.
I en triangel är längden av sidorna 68 cm, 285 cm och 293 cm. Är triangeln rätvinklig? Motivera ditt svar.
Svar: Ja, eftersom 682 + 2852 = 2932.
Rita en skiss av två olika rätblock och sätt ut mått på kanterna. Rätblockets volym ska vara 400 cm3.
Två exempel: 4 cm x 10 cm x 10 cm och 5 cm x 8 cm x 10 cm.
Hur stor är vinkeln a, b och c?
Svar: a = 50° , b = 60° , c = 70°
Vad är längdskalan om en sträcka i verkligheten är 4,2 km och motsvarande längd på en karta är 35 cm?
Svar: 1:12 000.
Filip råkar tvätta sin tröja för varmt och den krymper med 15 % på både längden, bredden och höjden.
Hur många procent mindre blir volymen av hans tröja efter att han tvättat den, i förhållande till hur volymen var innan tvätten? Avrunda till hela procent.
Svar: Volymen blir ungefär 39 procent mindre.
Beräkna längden av sidan x. Alla mått är i cm.
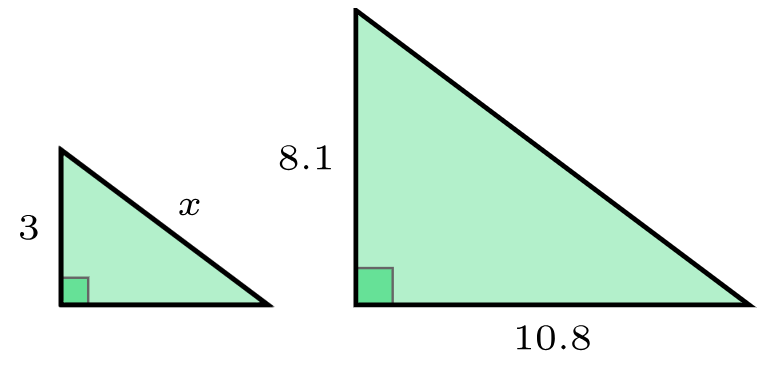
Svar: 5 cm.
Storleken på en TV-skärm mäts i tum och anger avståndet mellan två diagonalt motsatta hörn. Beräkna höjden av en 50 tums TV-skärm som har bredden 112 cm. En tum motsvarar 2,54 cm. Svara i hela cm.
Svar: 60 cm.
Den stora Peterskyrkan i Rom har en kupol i form av ett halvklot vars högsta punkt ligger 120 m över golvet. Kupolens diameter är 42 m. Se bild nedan.
a) Beräkna den totala volymen av luften i kupolen och i det cylinderformade rummet under den. Avrunda ditt svar till tusental kubikmeter.
b) Varje kubikmeter luft väger 1,23 kg. Hur mycket väger luften i denna del av Peterskyrkan? Svara i ton (1 ton = 1 000 kg).
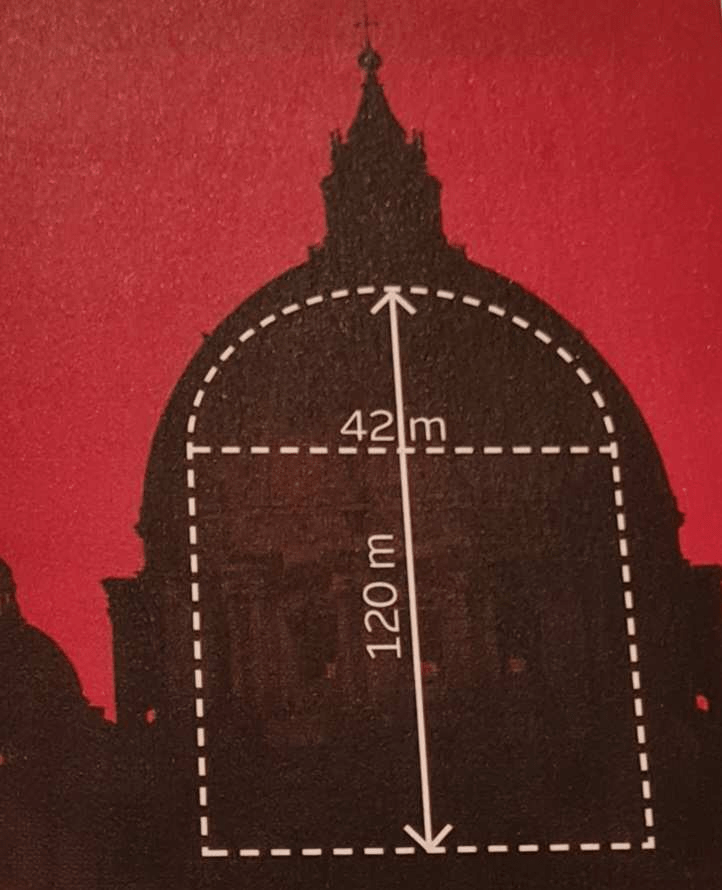
Svar: a) 156 000 m3, b) 192 ton.
Hur stor andel av området är skuggat?
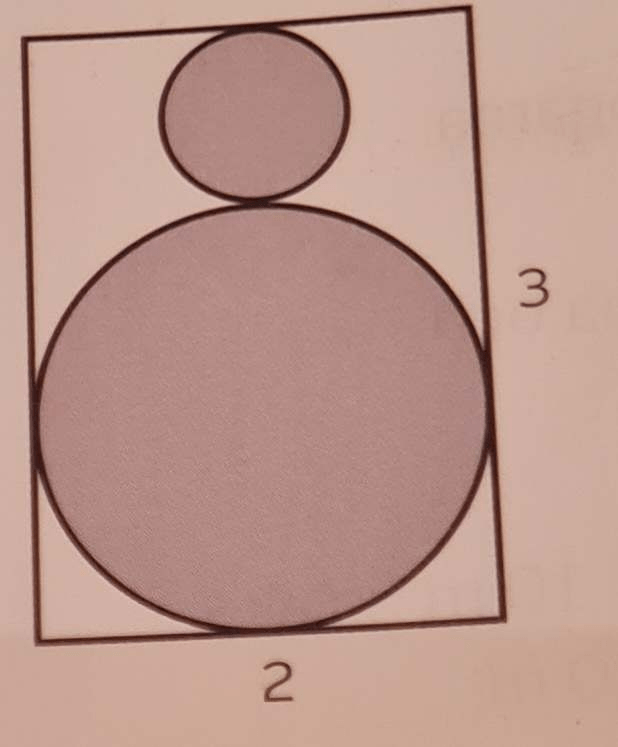
Svar: 65,4 %.
Utmaning: Diametern på en jordglob är 40 cm. Omkretsen på vårt jordklot är 4 000 mil. Beräkna vilken volymskala jordgloben är tillverkad i.
Svar: 1:3,2 × 1022
Martin har en stor Sverigekarta på väggen. Han har uppskattat arean på Sverige på sin karta och får den till 0,7 m2. Martins karta har längdskalan 1:800 000.
Martin har tänkt beräkna Sveriges verkliga yta utifrån denna information. Hjälp honom att göra detta och svara i kvadratkilometer.
Svar: 448 000 km2.
Beräkna längden av sidorna x och y.

Svar: x = 14 cm; y = 36 cm.
Beräkna arean av den gröna ytan. Avrunda till närmsta heltal.
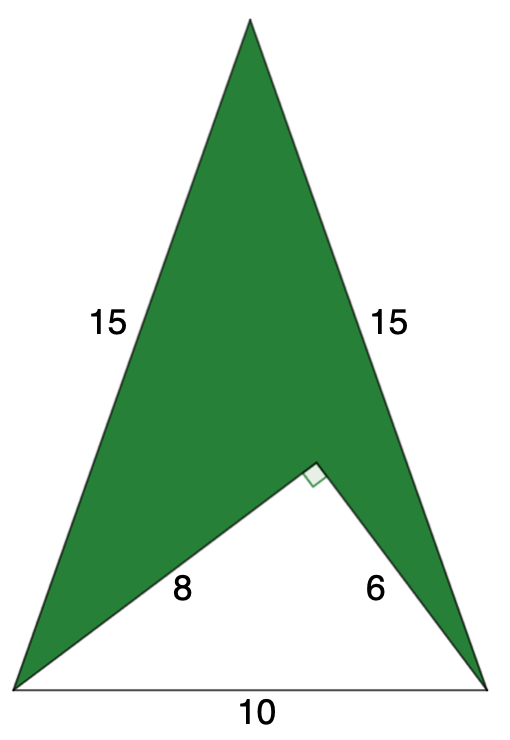
Svar: 47 cm2.
Inre diametern i en silverring är 1,1 cm. Ringens tjocklek är 1 mm och bredden är 4 mm. Hur mycket väger ringen? Densiteten för silver är 10,49 g/cm3.
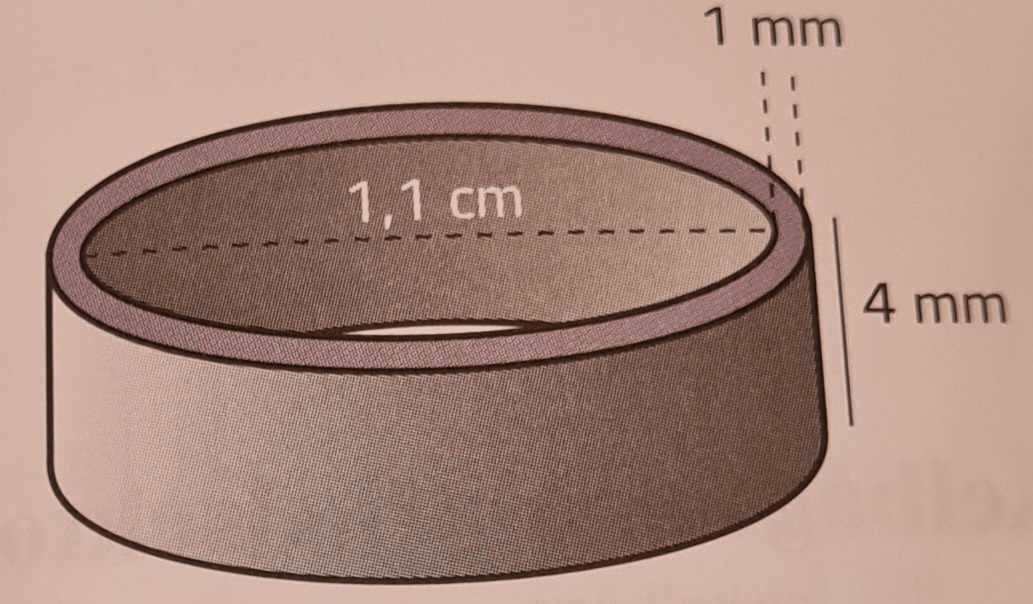
Svar: 1,6 g (1,58 g).
I en parallellogram är en vinkel tre gånger så stor som en annan vinkel i samma parallellogram. Hur stora är dessa vinklar?
Svar: 45° och 135°.