Cherry's Questions!
Vocab
Random Math
Probobiesty
NO
100
What is the probability of rolling a 5 and then a 2 on a die? As a fraction
1/36
100
What we expect to happen mathematically
Theoretical Probability
100
Solve 27x11 in 5 seconds!
The answer is 297! If you want to know how to solve a multiplication equation that has an 11 in it in 5 seconds, I can demonstrate it for you!
100
What is the probability that a caller will call your corner in 4 corners?
1/4(25%)
100
What are two things you can never eat for breakfast?
Lunch and Dinner
200
After repeated trials, the experimental probability should get _________ to the theoretical probability
closer
200
the ratio of the number of ways an event can occur to the total number of equally likely outcomes
Theoretical Probability
200
Can 2=1?
a=b
a2=ab
a2-b2=ab-b2
(a+b)(a-b)=b(a-b)
a+b=b
2b=b
2=1
Now, can you find the flaw in the logic that led to the conclusion that 2=1? The Solution: Remember if a=b, then a-b is zero. Now the first four equations led up neatly to the introduction of that term. And the next equation calls for dividing each side by (a-b) but dividing by zero isn't possible--and so are the chances of getting 2 to equal 1.
200
Ifan rolls a fair dice, with sides labeled A, B, C, D, E and F. What is the probability that the dice lands on a vowel?
Vowels: A E I O U
1/3
200
What is always coming but never arrives?
Tomorrow
300
What is the probability of not drawing an ace from a deck of cards?
92/100
300
Events that have no influence on each other
Independent
300
Three friends have a meal in a restaurant and they are charged $25. They each chip in with a $10 bill and hand it to the waiter. The waiter, though, isn't very good at math (like dividing the $5 change by 3), so he keeps $2 as a tip and hands each friend $1. Everyone seems pretty happy with the deal until one of the friends starts thinking about it. The three of them paid $10 each but got $1 back, so that meant that they spent $9 each. And since there were three of them, the total was 3 x $9, or $27, plus the $2 tip for the waiter. That takes the total to $29. What happened to the missing dollar?
This mystery is an excellent example of why it is important to read things carefully-in math and in other subjects. The trick here are the words "plus the $2 tip for the waiter." Instead of adding the $2 ("plus the $2 tip"), you should subtract it. Think about it. Subtract that $2 and you get $25, which is the amount the restaurant got. Each friend got $1 and the waiter got $2. Another way of thinking about it is to remember that the friends also shared the cost of the $2 tip ($0.67 each). So they paid $9 for their share of the meal and their share of the tip. The food itself cost each friend $8.33, then the $0.67 tip took that to $9. So if each paid $10 and got $1 back, then everything really does work out.
300
Which two answers cannot be a probability?
a) -0.00001
b) 0.5
c) 1.001
d) 0
e) 1
f) 20%
a and c. A probability has to be between 0 and 1, so a and c are the correct answers.
300
A girl fell off a 50-foot ladder but didn't get hurt. How?
She fell off the bottom step.
400
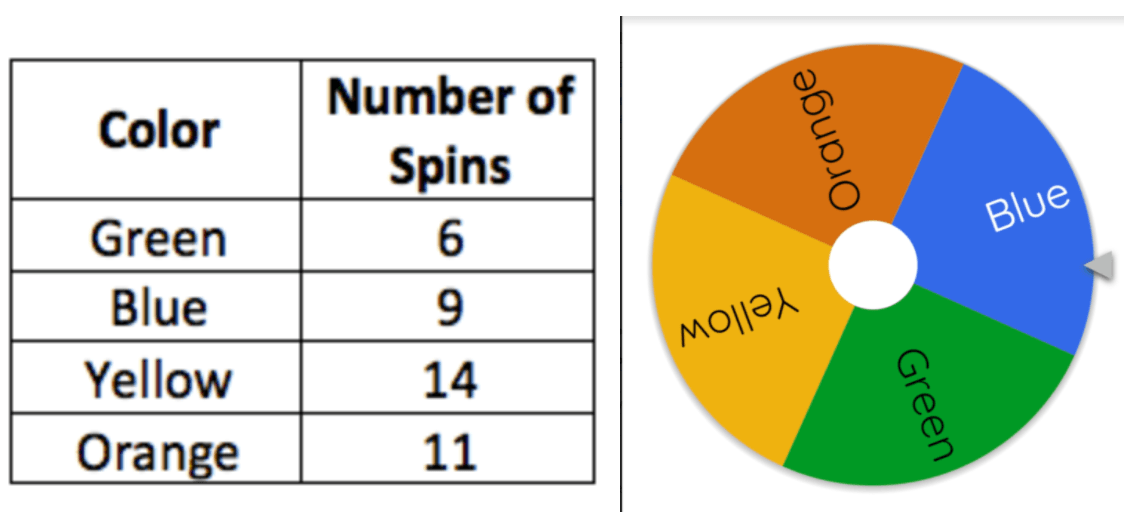
What is the theoretical probability of landing on green or blue?
1/2(50%)
400
The ratio of actual outcomes to the total number of possible outcomes in repeated trials
Experimental Probability
400
One of the best stories in math history involves a hot-tempered teacher and a boy genius. German mathematician Carl Friedrich Gauss was only seven years old for his first math class. His teacher, Mr.Buttner, liked to give really hard assignments. Mr.Buttner told the children to find the sum of the numbers 1 to 100. He sat down, saw to a few things on his desk, and then looked up and saw the children busy scribbling away on their slates. That is, all except one. Carl was sitting quietly with his hands folded. The slates Mr.Buttner collected were crammed full of numbers and crossings-out. Again, Carl's was the exception. His slate simply read 5,050-the correct answer! How'd he do it?
Like many other great thinkers, Carl could find simple solutions. He quickly realized that the sum of the first number and the last number (1 and 100) is 101. Likewise, the sum of the second number with the second-to-last number (2 and 99) is also 101. if he continued in this pattern, each pair adds up to 101. There are 50 pairs, so the total is 50 x 101 = 5,050. Simple!
400
How do you make the word "one" disappear?
Just add a g to the front-and now it's gone!
500
"84% of smokers have tried to quit"
What is the probability that someone who smokes does not want to quit? (84/100=84%;))
16%(16/100)
500
The second event is influenced by the first event
Dependent
500
Quick! Here's a math riddle.
Use four 9s in a math equation that equals a hundred.
Could you figure it out in 2 minutes or less?
Answer: 99+(9/9) = 100
500
If you have a bowl with six apples but then took away four, how many do you have?
you have four