Z-Score Basics
Interpret Z-Scores
z-score Applications
Properties of Normal Distribution
100
What does it mean if a z-score is 0?
The data value is the mean.
100
Interpret the z-score of 2.08 for an IQ score of 140.
An IQ score of 140 is 2.08 standard deviations above the mean.
100
In recent years, it was found that teenagers between ages 13 - 17 send/receive an average of 1740 text messages per month with a standard deviation of 550 text messages.
What is the z-score for a teenager who sends/receives 2150 text messages per month?
0.75
100
Why is this not a normal distribution?
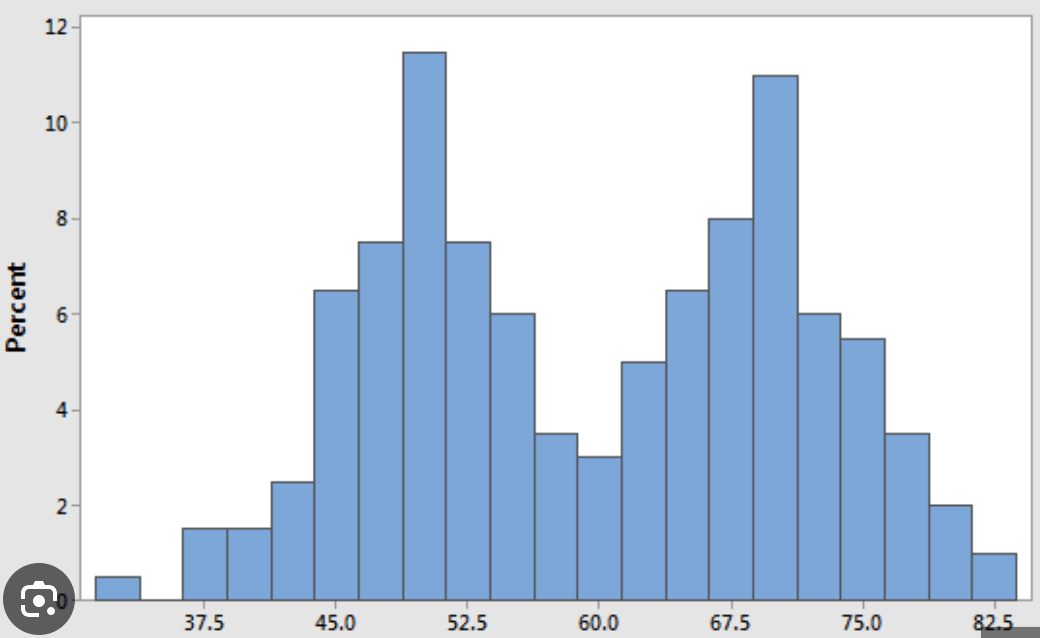
It is bimodal while Normal distributions are unimodal.
200
What does it mean if a z-score is positive?
The data value is above the mean.
200
Interpret the z-score of -2.5 for an exam score of 68 on a statistics exam.
A score of 68 is 2.5 standard deviations below the mean.
200
The Virginia Cooperative Extension reports that the mean weight of yearling (1-yo) Angus cattle is 1150 lbs. with a standard deviation of 80 lbs.
What is the z-score for a cow weighing 980 lbs.?
-2.13
200
Why is this not normal?
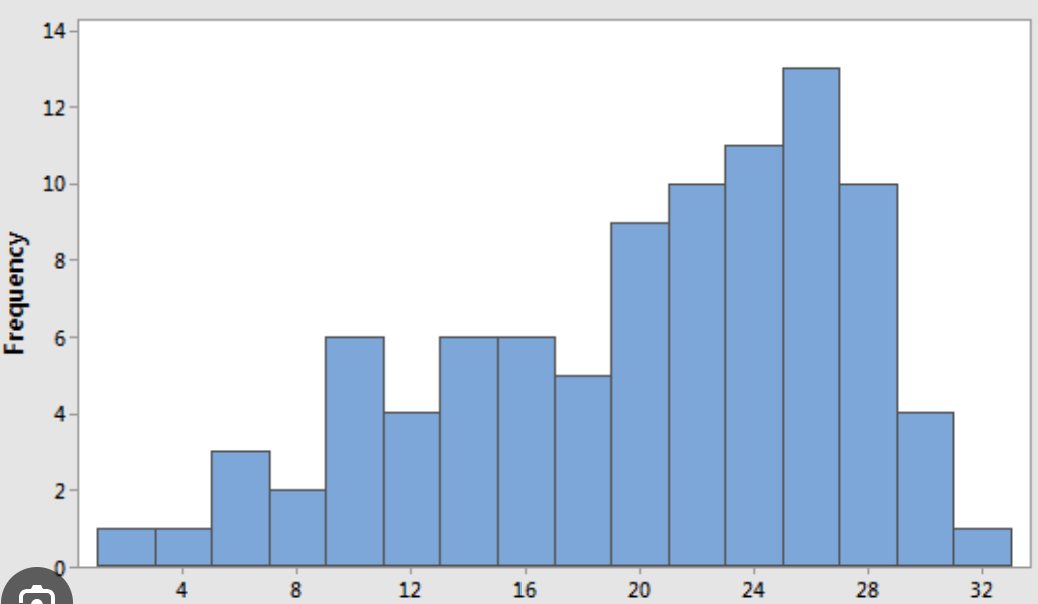
This is skewed left and Normal Distribution is symmetrical.
300
What does it mean if a z-score is negative?
The data value is below the mean.
300
If Martha scores a 64 on the history exam, interpret the z-score of -5.5 for her exam.
A score of 64 is 5.5 standard deviation below the mean.
300
In recent years, it was found that teenagers between ages 13 - 17 send/receive an average of 1740 text messages per month with a standard deviation of 550 text messages.
If a teenager has a z-score of 1.38, about how many text messages did he or she send/receive that month?
2499
300
Why is this not normal?
This is uniform and Normal is unimodal
400
Define z-score in your own words.
A z-score represents the number of standard deviations a data value is away from the mean.
400
Interpret the z-score of 0.75 for a teenager who sends/receives 2150 text messages per month.
2150 text messages is 0.75 standard deviations above the mean.
400
The Virginia Cooperative Extension reports that the mean weight of yearling (1-yo) Angus cattle is 1150 lbs. with a standard deviation of 80 lbs.
Is a cow weighing 1340 unusual? Explain.
Yes. The z-score is more than 2 s.d. from the mean.
400
Based on the given mean, median, and mode, can the distribution be normal?
Mode = 5
Median = 4
Mean = 3.5
No because the mean, median, and mode are the same in a Normal distribution.
500
Give the formula for calculating a z-score.
z = (x - mean) / sd
500
Interpret the z-score of -2.13 for a cow weighing 980 lbs.
A cow weighing 980 lbs is 2.13 standard deviation below the mean.
500
Give the formula to determine the data value associated with a given z-score.
x = (z)(s.d.) + mean
500
What happens to the Normal curve as the standard deviation increases?
The larger the standard deviation, the more spread out the data is so the shorter the curve.