Definitions
Basic Calculations
Choosing an Equation
Kinematic Calculations
Getting Direction on Acceleration
100
Speed
How fast something moves OR the distance an object covers per unit time.
100
Your cat, chasing a laser, darts 4 meters rightward, 3 meters leftward, another 4 meters leftward, and finally 2 meters rightward. What distance did your cat cover during his laser chase, which took a total of 5 seconds?
Distance = the total amount of travel, regardless of direction so we just add all your cat's movements together without using + or - signs in front of each value.
Distance = 4 + 3 + 4 +2
Distance = 13 meters
100
Write the equation you would need to use to solve for your unknown in the following situation. You do not need to solve the equation.
You found that your buggy cart in the lab we did travels at a constant speed of 0.4 m/s. What is the distance your buggy would cover if it is allowed to run across the floor for 5 seconds?
We are given speed and time and asked to determine the distance, so our equation should have speed, distance, and time in it.
S = D/t
*there is also no acceleration in this equation, so that clues us in that we should use a basic, not kinematic, equation.
100
A car coasts into a hill at 14.0 m/s. It slows down with a uniform acceleration of -1.0 m/s/s. What is the car's speed after 7 seconds?
Know:
v0 = +14.0 m/s
a = -1.0 m/s/s
t = 7 s
Trying to find v
Irrelevant quantity is displacement.
We can use v = v0 + at
v = 14 + (-1.0)(7)
v = 14 + -7
v = +7 m/s
100
A downward falling skydiver is speeding up. What is the direction of the skydiver's acceleration?
Direction of motion is downward.
Diver speeds up, so acceleration and velocity directions must agree.
Acceleration is downward.
200
Scalar
A quantity with only magnitude and no direction
200
Your cat, chasing a laser, darts 4 meters rightward, 3 meters leftward, another 4 meters leftward, and finally 2 meters rightward. What displacement did your cat have during his laser chase, which took a total of 5 seconds?
Displacement is a straight line connecting where something started to where it finished. We are given his different movements and direction of each movement, so we can add an appropriate +/- to each movement to make them his individual displacements and add them together to come up with his total displacement.
Assume + is rightward and - is leftward.
displacement = 4 + -3 + -4 + 2
displacement = -1 m
or 1 meter leftward from his starting point
200
You are cruising along I-95 at 30 m/s and go into the left lane to speed up to 35 m/s to pass someone. You speed up over the course of 3 seconds. What was your acceleration?
We know initial and final velocity, and time. We are trying to solve for acceleration. The appropriate equation would be...
v = v0 + at
200
A sports car traveling at 29.0 m/s slows to a velocity of 12.1 m/s over 10.6 s. How far does it move during this time?
We know...
v0 = +29.0 m/s
v = +12.1 m/s
t = 10.6 s
We are trying to find displacement.
Acceleration is our irrelevant quantity.
We can use x = (v0 + v)t /2
x = (29.0 + 12.1)(10.6) / 2
x = +217.8 meters
200
A downward falling skydiver is slowing down.
Direction of motion is downward.
Diver is slowing down, so acceleration and velocity have to be opposite directions.
Acceleration is upward.
300
Vector
A quantity with both magnitude and direction.
300
Your cat, chasing a laser, darts 4 meters rightward, 3 meters leftward, another 4 meters leftward, and finally 2 meters rightward. What was your cat's average speed during his laser chase, which took a total of 5 seconds?
speed = distance / time
Distance = the total amount of travel, regardless of direction so we just add all your cat's movements together without using + or - signs in front of each value.
Distance = 4 + 3 + 4 +2
Distance = 13 meters
Time is given as 20 seconds
S = D/t
S = 13 meters / 5 seconds
S = 2.6 m/s
300
You are running and suddenly skid to a stop in 1.5 seconds. You measure the skid marks you left on the ground to be a total of 2.7 meters. At what speed were you running at?
We are given time, displacement, and can assume final velocity is 0 m/s. We are trying to determine initial velocity. We can use...
x = (v0 + v)t/2
300
Cynthia competes in luge competitions during the winter months. During the initial stage of one downhill luge, Cynthia accelerated from rest at 6.89 m/s/s for 2.80 seconds. Determine the distance she moved during this acceleration phase.
We know...
v0 = 0 m/s
a = +6.89 m/s/s
t = 2.80 s
We are trying to determine displacement.
Final velocity is our irrelevant quantity.
We can use x = v0t + 1/2at2
x = (0)(2.80) + 1/2(6.89)(2.8)2
x = 1/2(6.89)(7.84)
x = +27 meters
300
A rightward moving bicycle is slowing down.
Direction of motion is rightward.
bicycle is slowing down, so acceleration and velocity have to be opposite directions.
Acceleration is leftward.
400
Velocity
How fast something moves in a certain direction OR the displacement of an object per unit time.
400
Your cat, chasing a laser, darts 4 meters rightward, 3 meters leftward, another 4 meters leftward, and finally 2 meters rightward. What was your cat's average velocity during his laser chase, which took a total of 5 seconds?
v = displacement / time
Displacement is a straight line connecting where something started to where it finished. We are given his different movements and direction of each movement, so we can add an appropriate +/- to each movement to make them his individual displacements and add them together to come up with his total displacement.
Assume + is rightward and - is leftward.
displacement = 4 + -3 + -4 + 2
displacement = -1 m
or 1 meter leftward from his starting point
Time is given as 5 seconds
Velocity = displacement / time
Velocity = -1 / 5
Velocity = -0.2 m/s or 0.2 m/s leftward
400
Starting from rest, a housecat is able to reach its top speed of 13.4 m/s in 3 seconds. What was the cat's acceleration through this motion?
We are given final velocity and time, and are able to infer initial velocity is 0 m/s (starting from rest). We are trying to determine acceleration, so we would use...
v = v0 + at
400
Rickey Henderson, baseball's record holder for stolen bases, approaches third base. He dives headfirst, hitting the ground at 7.59 m/s and reaching the base at 4.90 m/s, accelerating at -5.03 m/s/s. Determine the distance Rickey slides across the ground before touching the base.
We are given:
v0 = +7.59 m/s
v = +4.90 m/s
a = -5.03 m/s
We are trying to find displacement.
Time is our irrelevant quantity.
We can use v2 = v02 +2ax
(4.90)2 = (7.59)2 + 2(-5.03)x
24.01 = 57.6081 + -10.06x
-33.671 = -10.06x
Divide both sides by -10.06
x = +3.3 meters
400
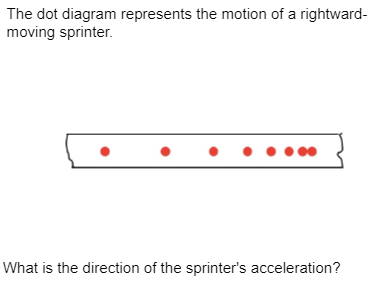
Sprinter is moving right.
Diagram shows sprinter's position values getting closer together, indicating he is slowing down.
Slowing down means acceleration and velocity must be in opposite directions, so acceleration is leftward.
500
Acceleration
How quickly something speeds up or slows down in a certain direction OR the rate of change of velocity per unit time.
500
Say your cat was running leftward at his top speed of 10 m/s and then skids to a stop in 2 seconds to catch the laser. What is your cat's acceleration?
We must determine both the magnitude and direction of your cat's acceleration, since acceleration is a vector quantity. To find magnitude, we use our acceleration equation.
a = change in velocity / time
a = 10 / 2 = 5 m/s/s
The direction of acceleration depends on the direction your cat is running in along with whether he is speeding up or slowing down.
Your cat is moving leftward and slowing down, so acceleration must be in the opposite direction as his velocity, making it rightward.
Our complete answer is...
a = 5 m/s/s rightward
500
A falcon is soaring through the air at 5 m/s when it spots a mouse 10 meters away. It speeds up to 7 m/s to when it catches the mouse. What was the falcon's acceleration?
We are given initial velocity, final velocity, and displacement. We are asked to find acceleration. We would need to use the equation...
v2 = v02 + 2ax
500
A bicyclist begins her descent down a hill moving with a speed of 2.79 m/s. She moves with a constant acceleration of 2.00 m/s/s. The hill is 42.4 m long. How long does it take her to reach the bottom of the hill?
We know...
v0 = +2.79 m/s
a = +2.00 m/s
x = +42.4 m
We are trying to find time.
Our irrelevant quantity is final velocity.
We can use x = v0t + 1/2at2
42.4 = (2.79)t + 1/2(2.00)t2
42.4 = 2.49t + t2
We have a t and a t2 in our equation, so we need to use the quadratic formula. To use the quadratic formula, we need to solve our equation for zero.
42.4 - 42.4 = t2 + 2.49t + -42.4
0 = t2 + 2.49t + -42.4
Now we need to determine what a, b, and c are. We can determine which number value in our equation goes with which letter by looking at the quadratic formula "template".
0 = ax2 + bx +c
a = 1
b = 2.49
c = -42.4
Now we plug these values into the quadratic formula and simplify.
(- b +/- sqrt (b2 - 4ac)) / 2a
(-2.49 +/- sqrt(2.492 - 4(1)(-42.4)) / 2(1)
(-2.49 +/- sqrt(6.2001 + 169.6)) / 2
(-2.49 +/- sqrt(175.8001)) /2
(-2.49 +/- 13.26) / 2
Subtraction option gives us -7.9 seconds
Addition option gives us 5.4 seconds.
5.4 seconds is the only option that makes sense since time is scalar and can't have a +/- sign
500
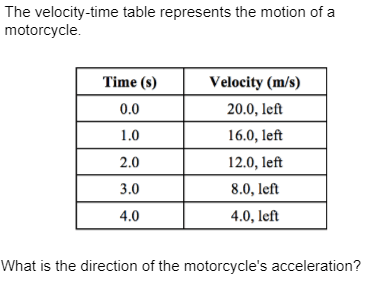
The direction of motion is given on the table as leftward.
We can see the numerical values for velocity are getting smaller as time goes on, so the object slows down.
Slowing down means acceleration and velocity are opposite directions, so acceleration is rightward.