1
2
3
4
5
100
4ab-7a+3b-12ab-4a+3b
-8ab-11a+6b
100
3a(2a-5b)
6a^2-15ab
100
See on võrrandisüsteemi lahendiks
Lõikepunkt
100
Tegurda
6m-am
m(6-a)
100
(27𝑎7𝑏5 − 9𝑎3𝑏) ∶ 3𝑎2𝑏
9𝑎5𝑏4 − 3𝑎
200
45a^6b^2c^5:(-5a^2bc^5)
-9a^4b
200
14a^3b^3(-3a-2ab^3)
-42a^4b^3-28a^4b^6
200
Esimene samm võrrandisüsteemi lahendamisel
Võrrandid kujul y=
200
Tegurda 4x-6xy
2x(2-3y)
200
Kuidas nimetatakse pildil olevat graafikut.
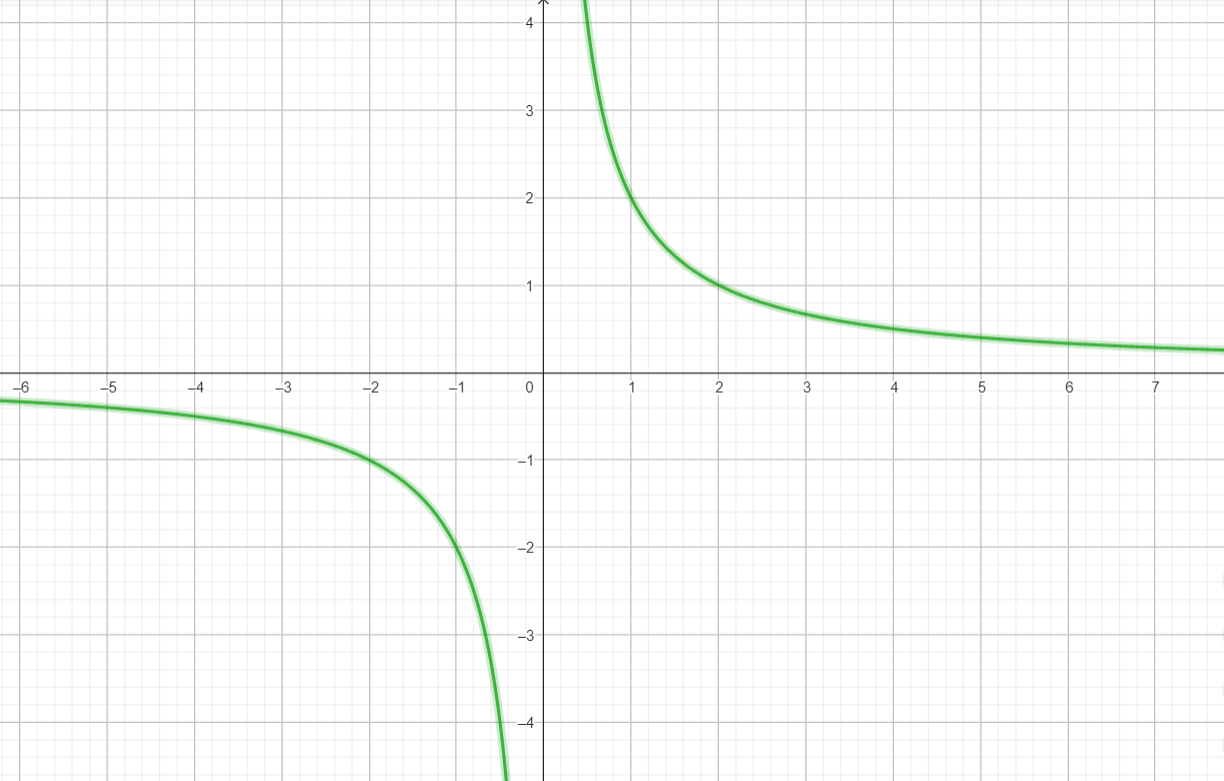
Hüperbool
300
(-6x^2y^3)^2
36x^4y^6
300
7𝑥𝑦(𝑥5 +𝑦6 −3)
7𝑥6𝑦 + 7𝑥𝑦7 − 21𝑥𝑦
300
x=2
y=4x-3, leia y-i väärtus
y=5
300
Tegurda 25a5b3-15a3b3-20a3b5
5a3b3(5a2-3-4b2)
300
Müts maksis 20€. Siis alandati hinda ja uueks hinnaks oli 15€. Mitu protsenti hinda alandati?
25%
400
(32a^2b^4-12ab^5+4ab) / (4ab)
8ab^3-3b^4+1
400
3n+(4m4n-6m3n2):(2m3n)
2m
400
Vii võrrand kujule y=
2x+y=16
y=16-2x
400
Tegurda 15a4b2c-5a3b3
5a3b2(3ac-b)
400
Lineaarfunktsioon y=2x+b läbib punkti A(1;3). Mis on vabaliikme väärtus?
b=1
500
(36𝑢12𝑣7 − 12𝑢5𝑣)∶12𝑢𝑣
3𝑢8𝑣6 − 𝑢
500
(-5/7x^6y^2z^5+1 1/9x^7yz^5):(5/12x^6yz^5)
-1 5/7y+2 2/3x
500
Vii võrrand kujule y=
2x-4y=16-2x
y=x-4
500
Arvuta
(25^2-25*19)/(20*12-40)
3/4
500
Paberilehes oli ristkülikukujuline auk, mille üks külg oli teisest kaks korda pikem. Sinna paberile joonistati neli ruutu nii, et neist iga üheks küljeks oli augu üks külgedest. Seejärel joonistati paberile neli ühesugust ristkülikut, mille kaheks küljeks olid erinevate suurustega ruutude küljed. Joonistatud neli ruutu ja neli ristkülikut värviti punaseks. Mitu korda oli punaseks värvitud osa pindala suurem augu pindalast.
9