What do you use to solve for b:
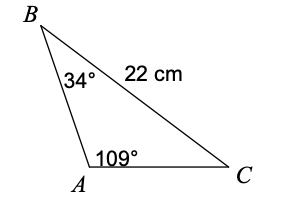
Law of Sines
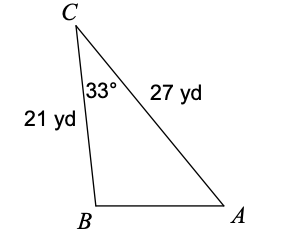
Find a:
a = 33.1 yd
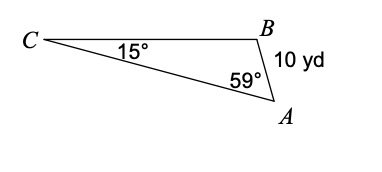
Find AB:
AB = 30.2 m
A hiker is lost in the woods and needs to find their way back to the trailhead. They know the distance to a landmark is 80 meters, the angle at the landmark is 30 degrees, and the angle at the trailhead is 60 degrees. Determine their distance to the trailhead.
46.2 meters
Find the area of the given triangle: 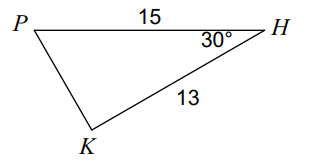
48.7 units2
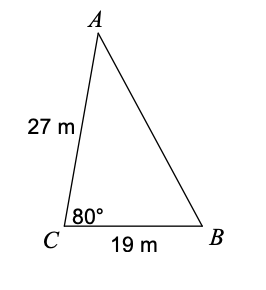
What do you use to solve for angle C:
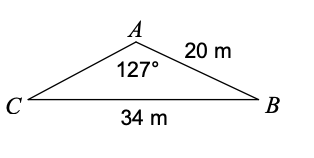
Law of Sines
Find angle A:
140
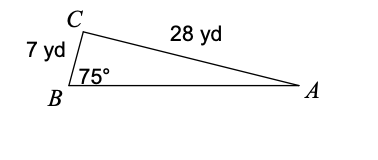
Find side c: 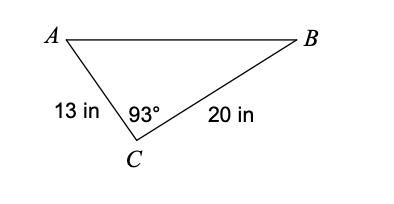
24.4 in
A construction crew is building a roof with a triangular top. They know the length of one rafter is 20 feet, the angle between the rafters is 80 degrees, and the angle between the rafter and the horizontal is 30 degrees. Calculate the length of the other rafter.
37.6 ft
Find the area of the triangle given:
34.1 units2
What would you use to solve for side c: 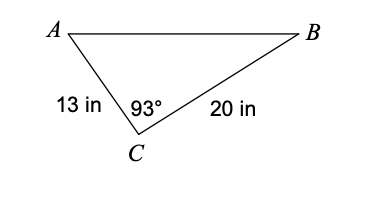
Law of Cosines
Find side a: 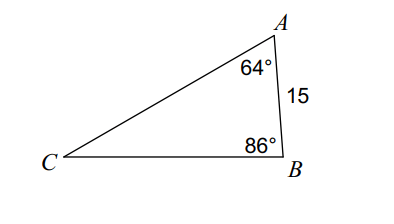
a = 27
Find angle C:
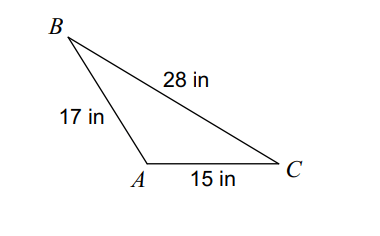
310
A construction crew needs to build a bridge across a lake but needs to know how long the bridge should be. A person walks from from edge of the lake 53 meters. He turns a 67-degree angle and walks 80 meters to the other end of the lake. How wide should a bridge be to go across this lake?
76.8 meters
Find the area of the triangle:
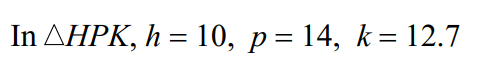
61.4 units2
Find the area of:
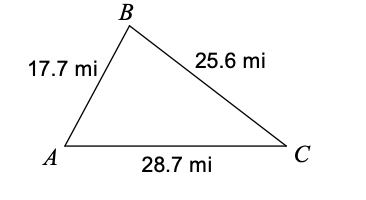
sqrt(s(s-a)(s-b)(s-c)
Solve the triangle for all missing parts:
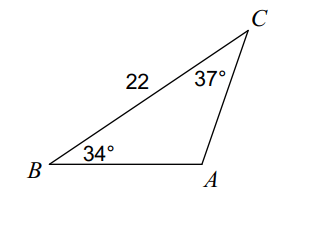
Angle A: 1080
b = 13
c = 14
Find angle A:
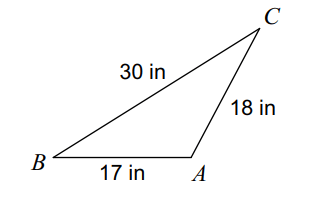
1180
A builder buys a triangular piece of land with sides 13 miles, 5 miles, and 12 miles. Find the area of his land.
30 miles2
Find the area of the triangle:
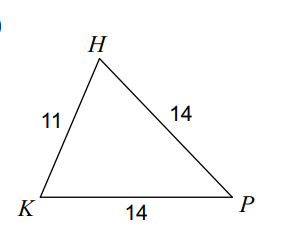
70.8 units2
Find the area of:
Area = 1/2(ab)sinC
Find TWO angle A's for the triangles in which:
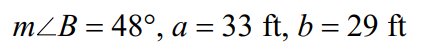
57.30 and 122.70
Solve a triangle if the sides are as follows:
a = 28 in, b = 15 in, c = 17 in
Remember to do law of cosines TWICE. Do not go back to law of sines.
A = 1220
B = 270C = 310
A builder buys a triangular piece of land with sides 13 miles, 5 miles, and 12 miles. He wants to fence in this land. What should the angles be of the fence? (There should be 3 angles as your answer.)
Find the area of the triangle:
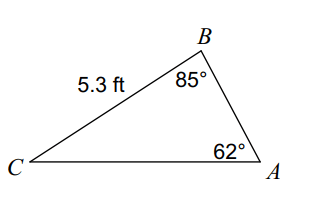
8.7 ft2