Population Structure & Growth
Discrete Individuals & Extinction
Spatial Structure of Populations
Metapopulation Capacity
100
What does the first row represent in the Leslie matrix? the diagonal? below the diagonal?
the first row: reproduction (m- fecundity)
the diagonal: survivorship (l)
below the diagonal: moving between stages (g- the probability of moving from one stage to the next)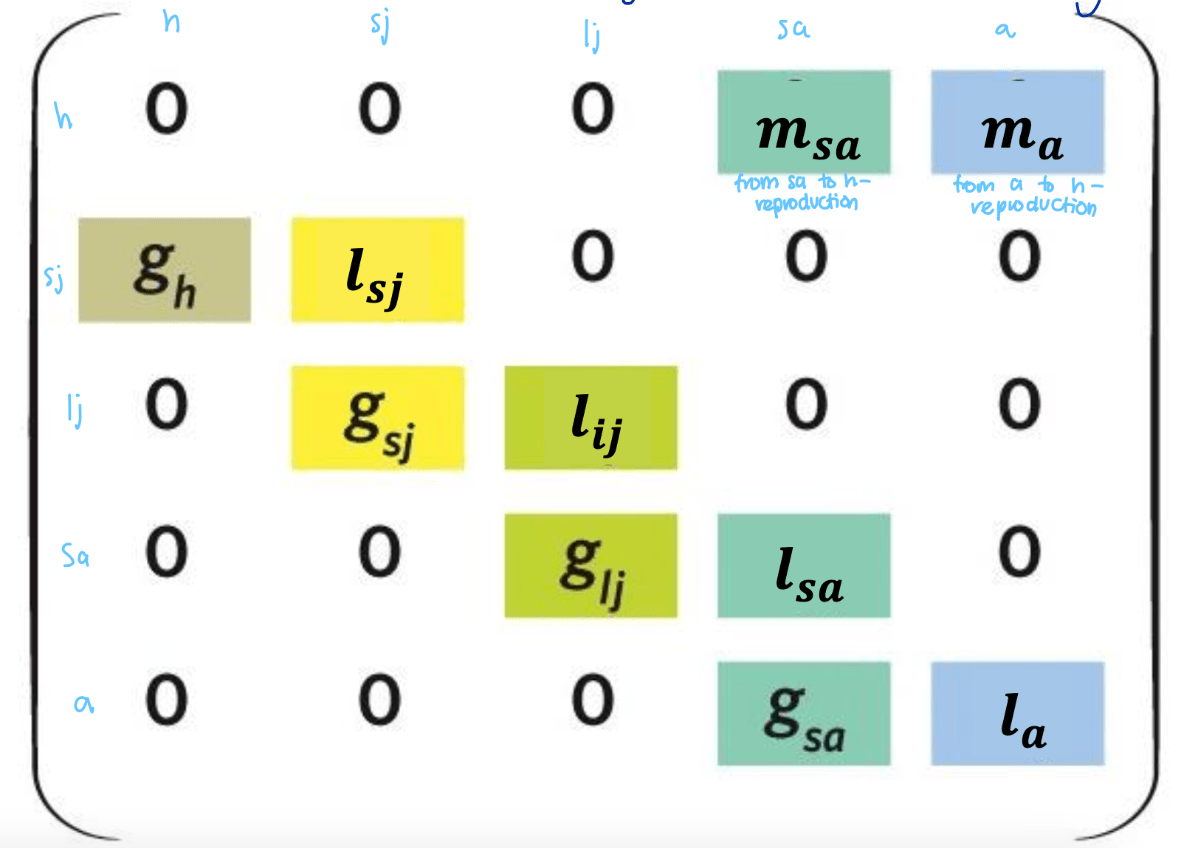
100
What is the big difference between abundance and density that we have ignored so far?
abundance is discrete (whole numbers) and density is continuous (not a whole number)
100
What is a metapopulation?
a set of populations (subpopulations) linked by dispersal that experience regular local extinction and recolonizations
100
What is the big difference between Levin's metapopulation model and Hanski's metapopulation model (metapopulation capacity)?
Hanski's is spatially- explicit and Levin's is spatially- implicit. Hanski's also takes area into account.
200
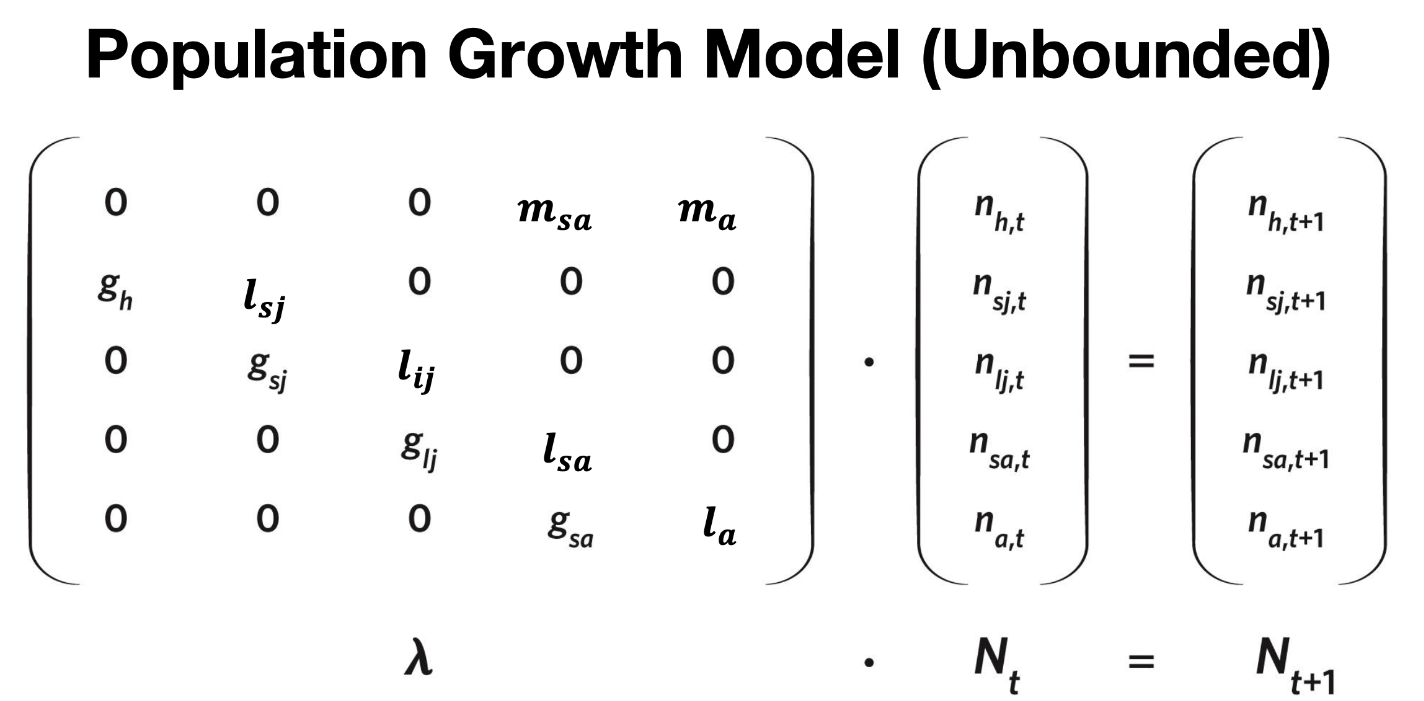
What is a Leslie matrix?
a population growth model (geometric) that accounts for population structure
- different numbers of individuals at different ages (or stages)
200
What is demographic stochasticity?
random variation in abundance because of the discrete nature of individuals
- individuals are discrete- whole numbers
200
When looking at metapopulations, instead of tracking population abundance- what does our focus switch to?
to habitat patches and whether or not they are occupied
p: the proportion of suitable habitat patches that are occupied
200
What is the influence of area on the probability of a population going extinct? (Hanski's)
extinction is a function of area-
smaller: more likely to go extinct
larger: less likely to go extinct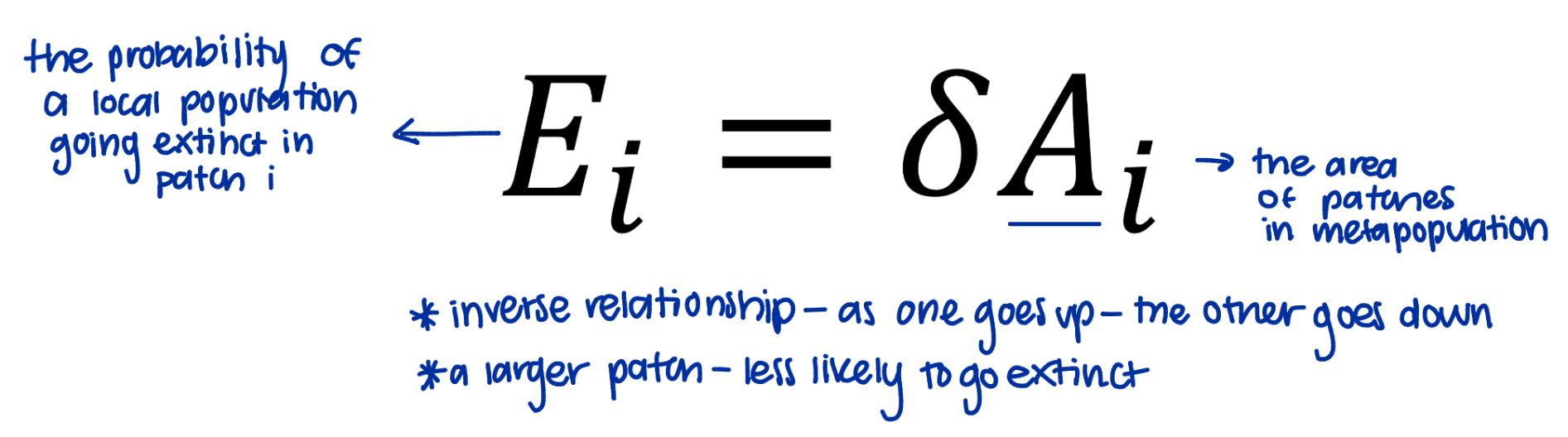
300
Using a Leslie matrix, how could you calculate the predicted population abundance for the next generation?
λ x N(t)= N(t+1)
- use matrix algebra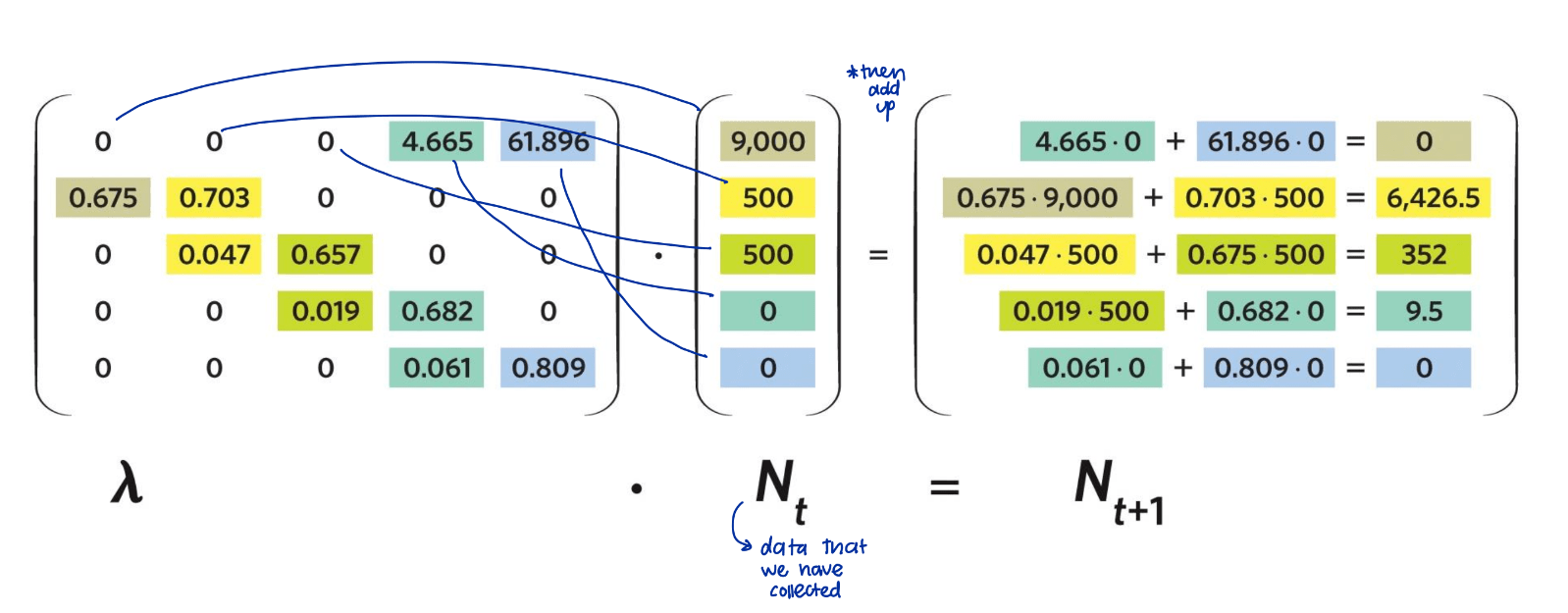
300
What is environmental stochasticity? What does it relax?
- it is the random variation in vital rates because of fluctuations in the environment
- it relaxes the assumption that birth rate and death rate are constant
300
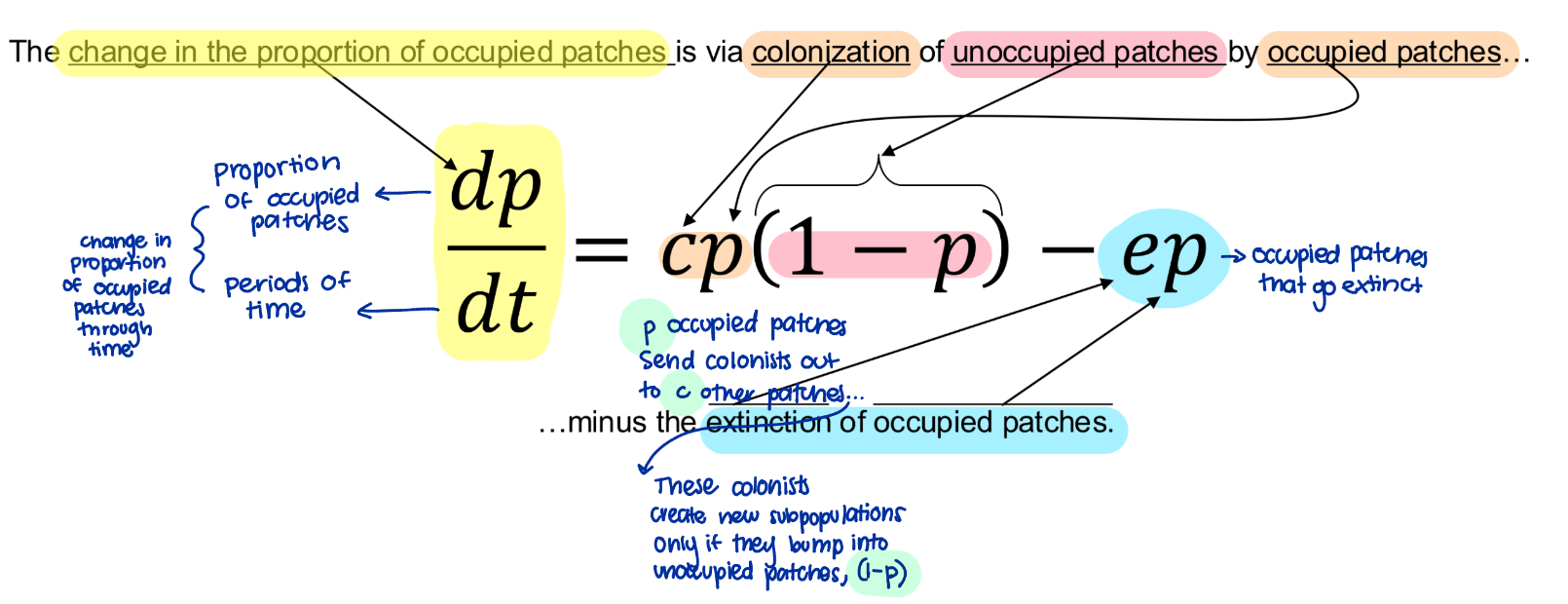
What does Levin's population model state?
the change in proportion of occupied patches is via colonization of unoccupied patches by occupied patches minus the extinction of occupied patches
300
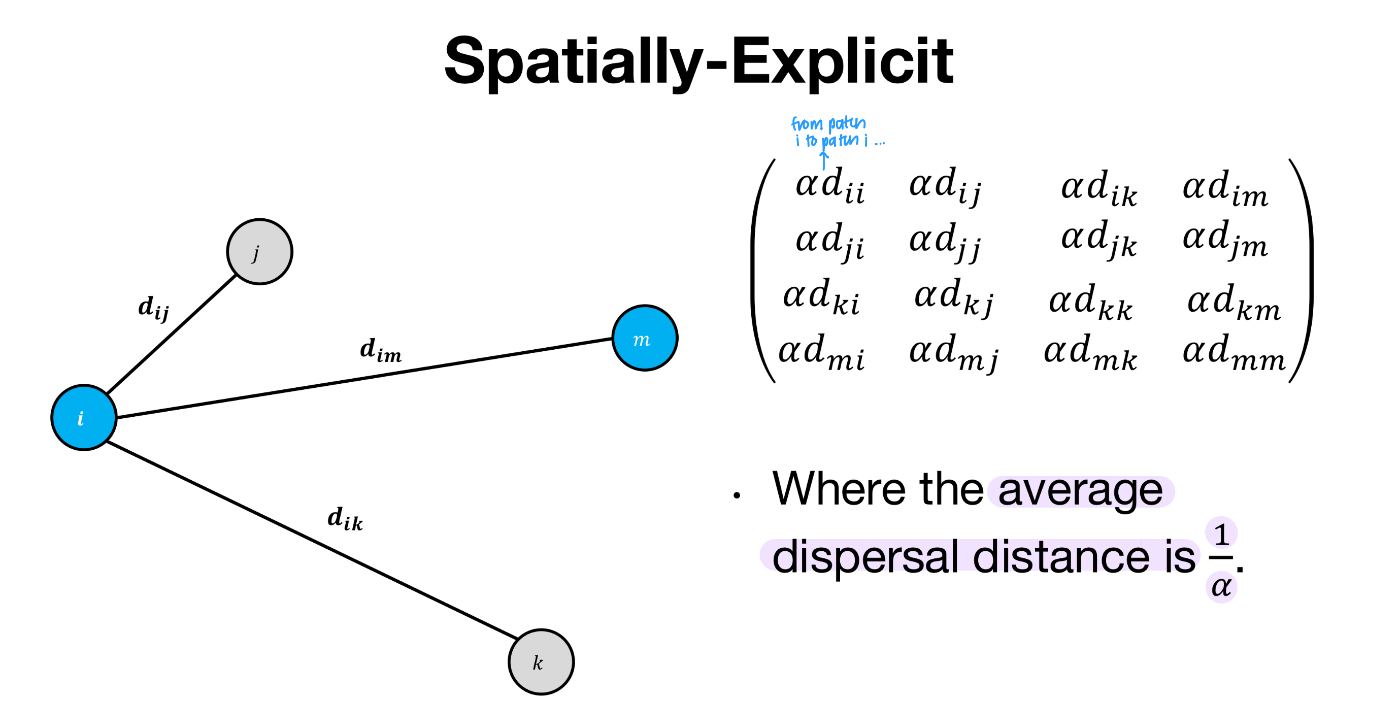
How do you create a spatially- explicit matrix?
- assume all patches are equally sized (ignore area)
- calculate the pairwise connections between patches
-organize into a matrix (using distance between patches and the average dispersal distance of the organism)
400
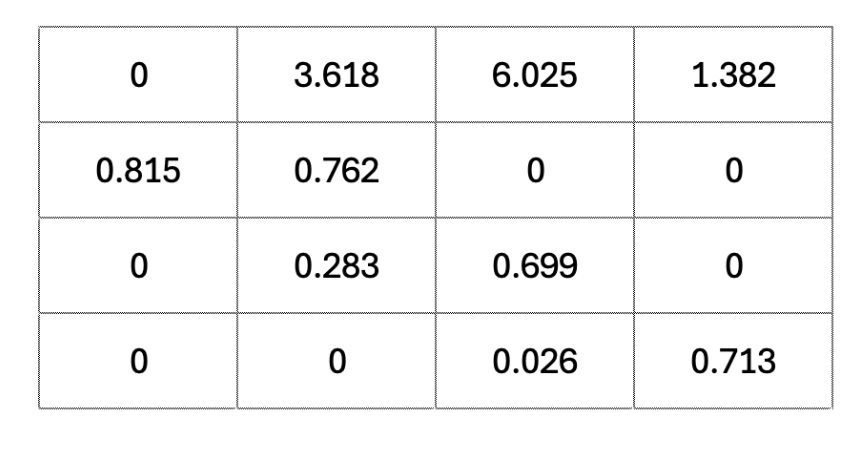
Construct a Leslie matrix from the information given.
400
In a closed system, what will stochasticity always lead to?
Extinction!
- If every closed population goes extinct, why do we observe populations persisting?
- We made an assumption that migration in and out were negligible, but this is not really the case. Migration can help prevent extinction and recolonize after extinction occurs.
400
What is Hanski's metapopulation model?
a spatially- explicit model where connectivity depends on the distance between patches and patch area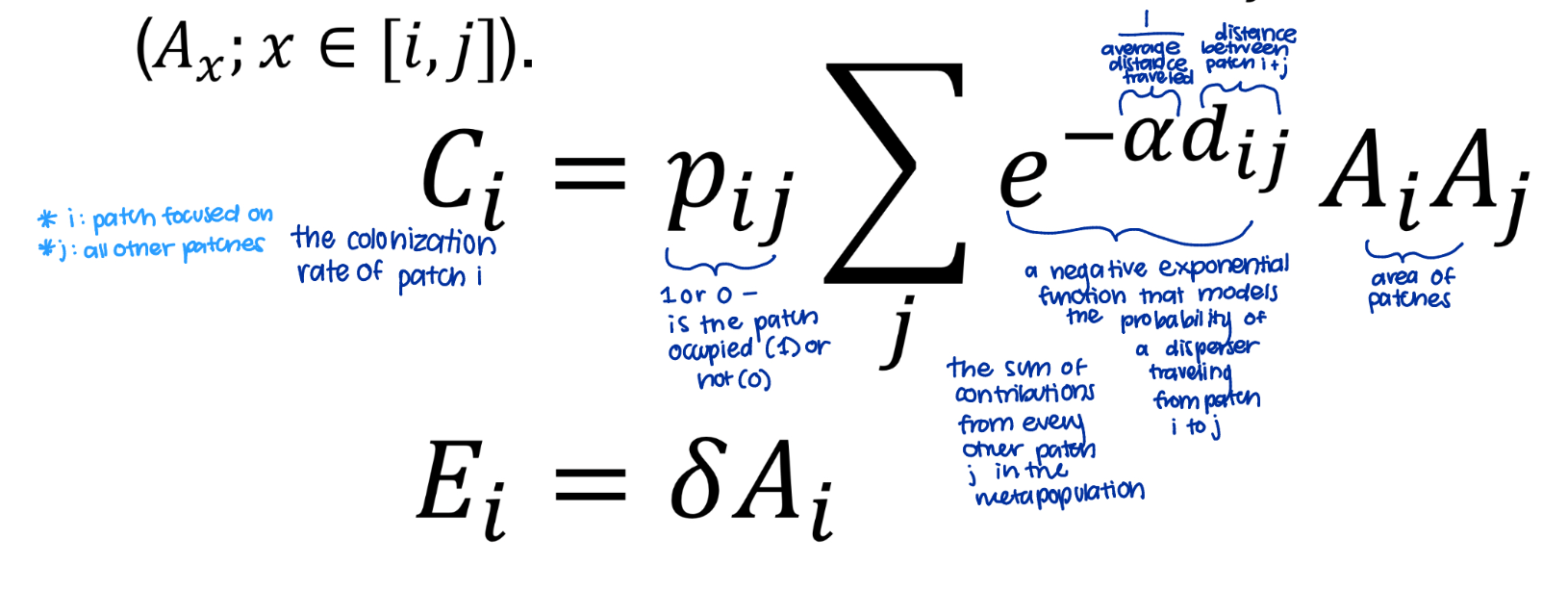
400
What is the point of a spatially- explicit matrix?
It can allow us to see the importance of each habitat patch.
- calculations can be done to tell us which patches are most important and how connected the system is, which could be important for conservation efforts