Is It A Function?
Evaluating Functions
Graphing
Random
200
How do you know if something is a function?
When every input goes to exactly one output.
200
Consider the function f(x) = 3x - 7. Find f(1).
f(1) = -4
200
Name three key features of graphs.
Increasing interval, decreasing interval, constant interval, positive, negative, x-intercept, y-intercept.
200
How do you pronounce the function f(x) = 2x2 - 1?
"F of x equals two x squared minus one"
400
Is this a function? Why or why not?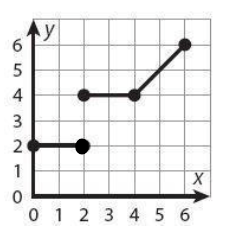
No- there are multiple outputs when the input is 2.
400
Consider the function f(x) = 3x - 7. Find x if f(x) = 23.
x = 10
400
An airplane takes off from the ground, increases in altitude quickly, flies at a constant altitude, increases in altitude more quickly than at first, and then stays at
the same altitude. Draw a graph to represent this situation.
400
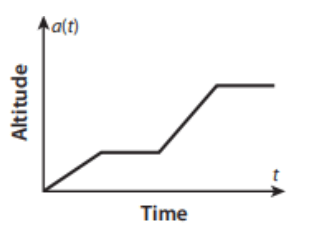
What do domain and range represent?
Domain: all possible x values of a function.
Range: all possible y values of a function.
600
Does this represent a function? Why or why not?
{(0, 0), (2, 9), (1, 10), (6, 9), (2, 0)}
No- there are repeated input values.
600
Alex tracks the number of different students he speaks to during the day. The value p(t) represents the total number of different students Alex has spoken to t hours after waking up at 4:00 am.
Is the following statement true or false?
"p(10) represents the number of different students Alex has spoken to by 9:00 am."
False- p(10) represents the number of students Alex has talked to in the 10 hours after 4am, which would be until 2pm.
600
How can you solve the equation 2x - 4 = 3x + 1 by graphing?
You could graph the functions f(x) = 2x - 4, and g(x) = 3x + 1, and their intersection point(s) would be your solutions.
600
What is the Vertical Line Test?
Placing a bunch of vertical lines on a graph, and if any of them pass more than one point, it is not a function.
800
Does the equation y=2x-1 represent a function? Why or why not?
Yes- for every number you plug in for x (input), you only get one y value (output).
800
Alex tracks the number of different students he speaks to during the day. The value p(t) represents the total number of different students Alex has spoken to t hours after waking up at 4:00 am.
Is the following statement true or false?
"t = 4.5 as a solution to p(t) = 16 means that at 4:30 pm Alex has spoken to 16 different students."
False- t=4.5 represents 4.5 hours after 4am, which would mean at 8:30am Alex has spoken to 16 different students.
800
A store is open from 9 am until 4 pm. Function c represents the number of customers in the store x hours after it opens. What domain makes sense in
this situation? (Write in interval notation)
0 ≤ x ≤ 7
800
Given the table below, find the average rate of change for the interval -2 ≤ x ≤ 0.
m = 1.25
1000
Does this description represent a function? Why or why not?
"The amount of money Emma earns, m, for mowing lawns g hours."
Yes- Every possible input (hours mowing) would only go to one output (money made).
1000
Alex tracks the number of different students he speaks to during the day. The value p(t) represents the total number of different students Alex has spoken to t hours after waking up at 4:00 am.
Is the following statement true or false?
"p(12) - p(6) represents the increase in the number of different students Alex has spoken to from 10:00am to 4:00 pm."
True- p(12) represents 4pm, p(6) represents 10am, and we are finding the difference between them.