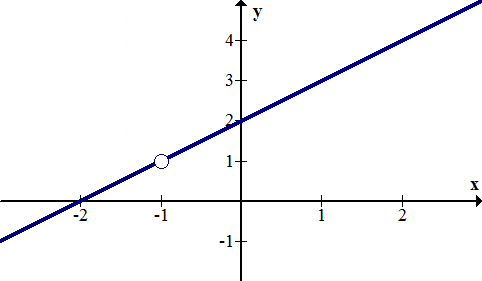
What are the 3 types of discontinuity?
-Jump
-Infinite
-Point/ removable
lim f(x)
x--> -1 -
1
A limit overall exists if...
The limits from the left and right side are equal.
What's the domain? Specify open or closed brackets.
(-infinity, +infinity)

f(3)=
1

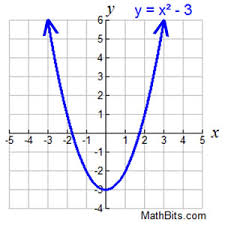
What type of discontinuity is shown?
Jump discontinuity

lim f(x)
x--> 1+
3
 lim f(x)
lim f(x)
x--> 3
2
 What's the domain? (Specify closed or open brackets)
What's the domain? (Specify closed or open brackets)
(-3, 1]
f(3)=
undefined

State the discontinuity type and its location.
Infinite discontinuity at x=3
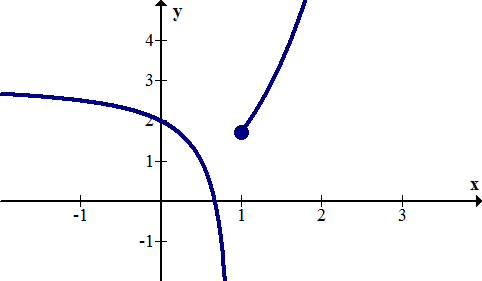
x--> 1-
neg. infinity
lim f(x)
x--> 1
DNE

What's the range? Specify closed or open brackets.
[-5, 4]
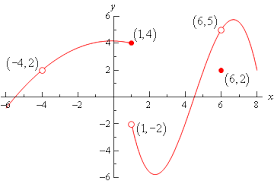
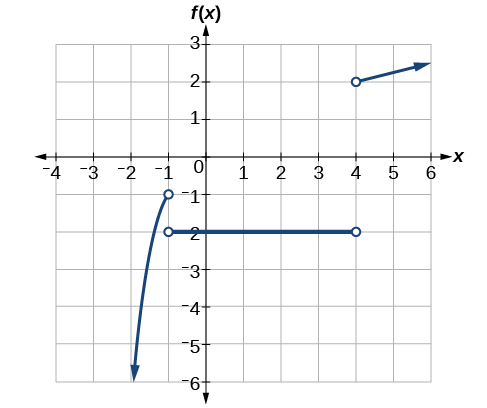 State the end behavior using limits.
State the end behavior using limits.
lim f(x) = -infinity
x--> -inf
lim f(x)= infinity
x--> +inf

At which x-values, is the graph discontinuous?
x=-4, 2, 4
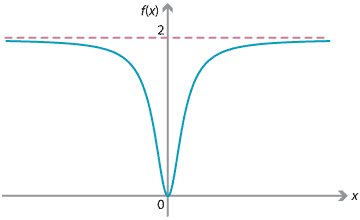
lim f(x)
x--> 0-
0
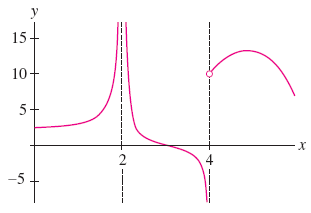
lim f(x)
x--> 2
infinity
 What's the range? Specify open or closed brackets.
What's the range? Specify open or closed brackets.
(-infinity, -1) U (2, infinity)
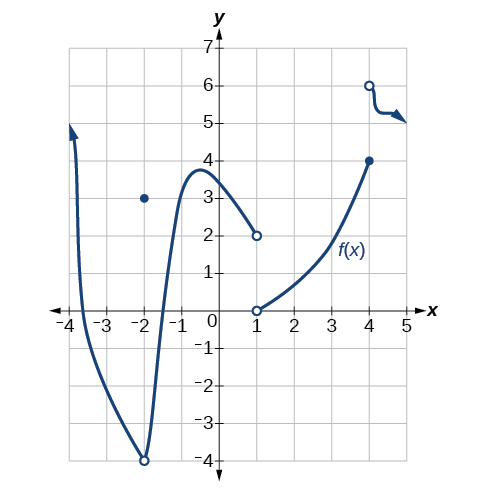 For what values of x is f(x)= 2 ... Estimate
For what values of x is f(x)= 2 ... Estimate
x=-3.8, -1.3, 3.1
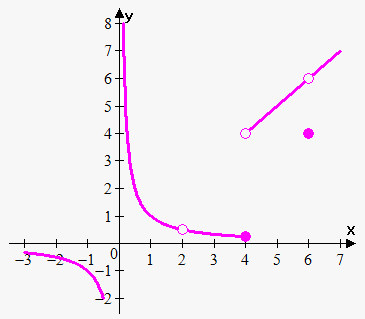
State the type(s) of discontinuity along with the location of each.
-Infinite at x=0
-Point at x=2
-Jump at x=4
-Point at x=6 (also jump)

lim f(x)
x--> 4+
4
lim f(x)
x--> 3
DNE
 What's the domain? Specify closed or open brackets.
What's the domain? Specify closed or open brackets.
(-infinity, -1) U (-1, 4) U (4, infinity)
State the increasing intervals of the graph.
(-infinity, -5) U (4, infinity)