Limits
Asymptotes
Discontinuity
End Behavior
Miscellaneous
100
lim_(x\to8)4/x
1/2
100
What are the vertical asymptotes of:
f(x)=4/(x^2-1)
x = 1 and x=-1
100
Where is the following function discontinuous?
f(x)=(x^2-4)/(x-2)
x=2
100
lim_(x\toinfty)(3x+2)/(5x-4)
3/5
100
lim_(x\to0)sin(x)/x
1
200
lim_(x\to2)(x^2+x-6)/(x^2-6x+8)
-5/2
200
What are the vertical asymptotes of:
y=(2x^2+2x+3)/(4x^2-4x)
x=0 and x=1
200
x<1: f(x)=4
x>1: f(x)=x^2+2
Is the function continuous at x=1?
No, f(x) is not continuous at x=1 because the left- and right-hand limits do not match (3 and 4, respectively)
200
lim_(x\toinfty)5+3/x
5
200
lim_(x\to0)(cos(x)-1)/x
0
300
lim_(x\to0)2e^x
2
300
What are the asymptotes of:
y=(x^2-9)/(3x-9)
There are none!
300
Is f(x) continuous at x=2?
x\ne2, f(x)=x^2
x=2, f(x)=1
No, f(x) is not continuous at x = 2.
300
lim_(x\toinfty)(5x+3)/(6x^2+4)
0
300
List the three conditions for proving continuity at a point:
f(a) \exists
lim_(x\toa^-)f(x)=lim_(x\toa^+)f(x)
f(a)=lim_(x\toa)f(x)
400
lim_(x\to0)(sin2x)/(3x)
2/3
400
What are the asymptotes of:
y=sin(x)
There are none!
400
Determine if the following function is continuous at x=-2:
f(x)= {x²+2x if x≤-2
x^3-6x if x≥-2.
The left hand limit is 0 and the right hand limit is 4. Since the left and right hand limits are not equal, a limit does not exist at x=-2.
400
lim_(x\toinfty)(5x^3-15)/(5x-5)
infty
400
The inequality for the IVT on [-2, 1] when proving f(x)=7 exists for:
f(x)=x^2+4
f(-2)>7>f(1)
500
lim_(x\to0)(x+sinx)/x
2
500
What are the vertical asymptotes of:
f(x)=tan(x)
x=pi/2, (3pi)/2, (5pi)/2, ...
500
On what intervals is the function continuous?
(x^2+3x+5)/(x^2+3x-4)
x\ne-4,x\ne1
OR
(-infty, -4),(-4, 1),(1,infty)
500
lim_(x\to-infty)(4x+3)/sqrt(x^2+2)
-4
500
Where does the limit not exist for the graph on the interval [-5, 4]:
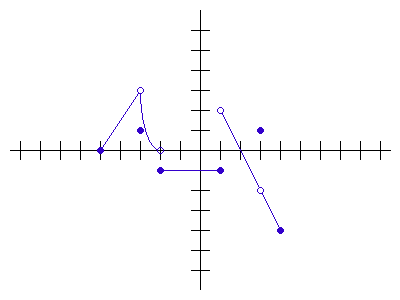
x=-2 and x =1