Determinants
Declaration of
Independence
Independence
Inverses and the IMT
Bases, Dimension, and Rank
Potpourri
100
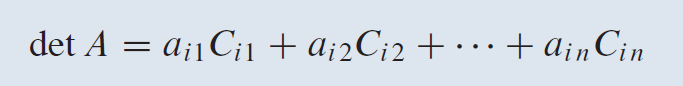
What is a cofactor expansion about the ith row?
100
The columns of a matrix A are linearly independent if and only if the equation Ax=0 has only this.
What is the trivial solution?
100
A matrix that does not have an inverse.
What is non-invertible?
Or: What is singular?
100
A basis for Rn must have exactly this many vectors.
What is n?
100
True or False:
Since matrix multiplication is not commutative in general, that is,
ABneBA
detAB ne detBA
What is FALSE:
Chapter 3.2 Theorem 6 states that
detAB=detBA
200
det[[a,b],[c,d]]
What is ad - bc?
200
A set of vectors {v1,v2, ...,vn} that is linearly dependent has these type of solutions to the equation:
x1v1 + x2v2 + ... + xnvn = 0
What are non-trivial solutions?
200
An invertible matrix has this type of determinant.
What is non-zero?
200
A set of basis vectors for Rn must have these properties (not including the fact that there are n vectors in the set).
What are:
1) Span Rn
2) Be linearly independent
(NOTE: The basis vectors MUST also be elements of Rn, but they will be if they span the vector space.)
200
For an mxn matrix A, the column space is a subspace of Rp for this value of p
What is p = m?
300
det[[1,0,0],[-2,1,-1],[2,1,4]]
What is 5?
300
A linear transformation T(x)=Ax that maps Rn to Rm has this property when the columns of the mxn matrix A are linearly independent.
What is one-to-one.
300
For an invertible matrix A, we are guaranteed a solution to the equation Ax = b for _____
b in R^n
What is "each" (or "every")?
300
True or False:
A plane in R3 can be completely defined by two R2 basis vectors
False
A plane in R3 can be defined determined by two R3 basis vectors
300
True or False:
For every p < n, where p and n are positive integers, Rp is a subspace of Rn.
What is FALSE.
It's not even a subSET. Rp and Rn do not contain the same dimension (size) vectors so they have no elements in common unless p=n.
400
(-1)i+j det(Aij)
What is a cofactor?
400
Chapter 1.7 Theorem 8 tells us that a set of p Rn vectors will be dependent if
What is p > n?
400
det[AB^-1]=
What is
detA/detB ?
400
The maximum rank of an mxn matrix A
What is min(m, n)?
400
The matrix below can be used to find the inverse of an invertible 3x3 matrix
[[C11,C21,C31],[C12, C22, C31],[C13, C23, C33]]
What is the adjugate matrix (or classical adjoint, or just adjoint)?
500
det[[1,0,0,1],[0,4,e,pi],[0,0,5,0],[1000,0,0,1006]]
What is 120?
500
For a square matrix A, the columns will be linearly independent if and only if its columns ____ Rn
What is span?
500
If A is an invertible matrix, then so are these matrices that are directly related to A.
What are: AT and A-1?
An acceptable alternate answer would be the matrix cA where c is any non-zero scalar constant.
500
500
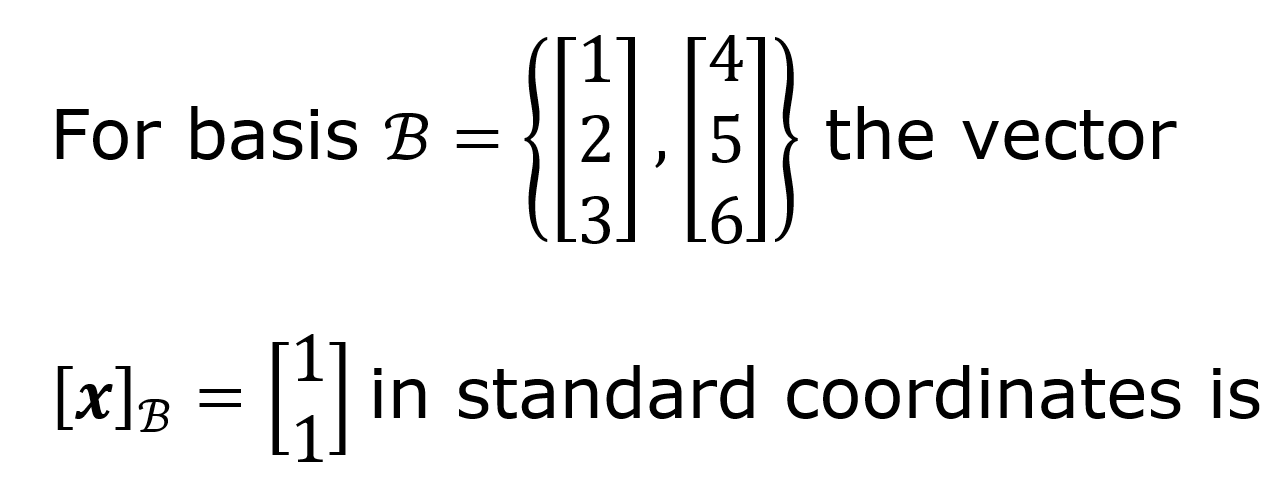
x=((5),(7),(9))