Find the point of interception
Finding the equation of a line 1
Finding the equation of a line 2
Find the slope
Miscellaneous
100
Solve the system of linear equations by graphing:
y = 2x + 9
y = -x + 6
(-1,7)
100
Find the equation of a line that passes through (0, 4) with a slope of -3
y=-3x+4
100
Find the equation of this line:
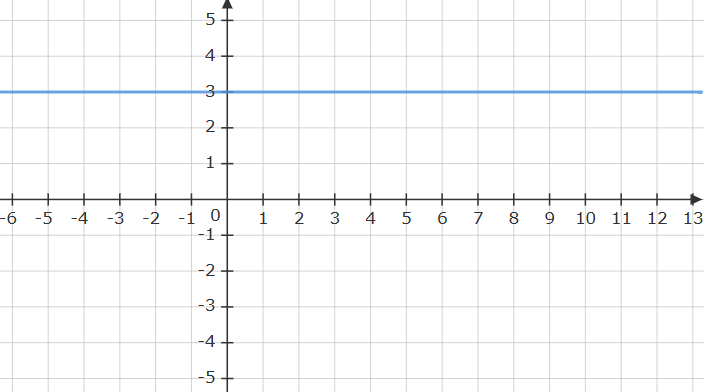
y=3
100
Find the slope of the line that passes through (0, 4) and (3, 0)
m=-4/3
100
Convert to y=mx+b
2x+y=10
y=-2x+10
200
Solve the system of linear equations by graphing:
y = x + 4
y = -x + 2
(-1,3)
200
Find the equation of a line that passes through (0,7) with a slope of 2
y=2x+7
200
Find the equation of the line
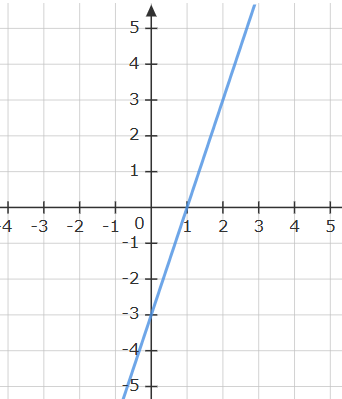
y=3x-3
200
Find the slope of the line that passes through (1, 2) and (2, 3)
m=1
200
Convert to slope-intercept form:
2x-2y=6
y=x-3
300
Solve the system of linear equations by graphing:
y = 2x + 5
y = 0.5x - 1
(-4,-3)
300
Find the equation of a line that passes through (-3, 7) with a slope of -2
y=-2x+1
300
Find the equation of the line
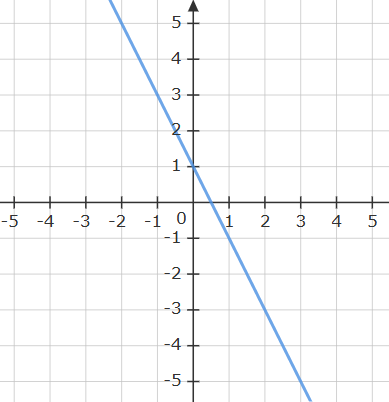
y=-2x+1
300
Find the slope of the line that passes through (-3, 4) and (-1, 4)
m=0
300
True or false, the point (-2, 4) lies on the line
y=-3x+5
False
400
Solve the system of linear equations by graphing:
x + y = 7
y = x + 3
(2,5)
400
Find the equation of a line that passes through (-1/2, 5) with a slope of 4
y=4x+7
400
Find the equation of the line:
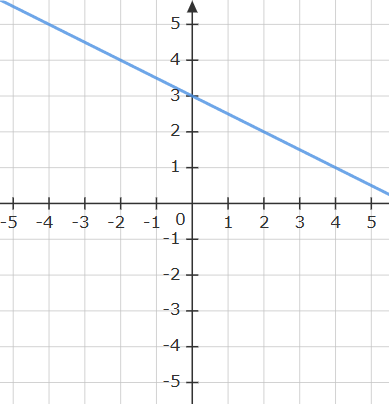
y=-1/2x+3
400
Find the slope of the line that passes through (-3, -6) and (-3, 5)
m = undefined
400
Does the point (-1, 7) lie on, above or below the line
y=-x+6
On
500
Is it possible for a system of linear equations to have exactly two solutions? Explain your reasoning.
No, two lines cannot intersect in exactly two points.
500
Find the equation of a line that passes through (-2/3, -7) with a slope of 9/2
y=9/2x-4
500
Find the equation of the line: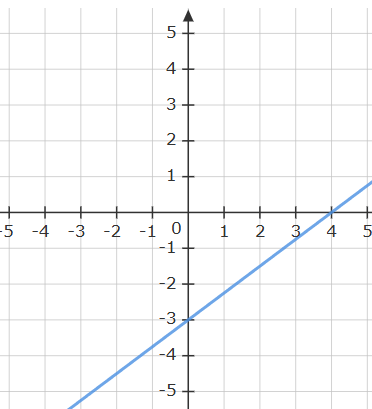
y=3/4x-3
500
Does the point (-1, 7) lie on, above or below the line
y=-2x+13
m=-7/5
500
Does the point (-4, 4) lie on, above or below the line
y=-2x-7
Above
4<1