Find x.
x + 8 = 7
x = -1
State whether this line has a positive, negative, zero or undefined gradient.
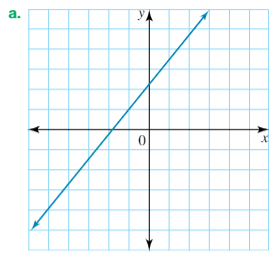
Positive
What does the "a" stand for in the linear form of y = bx + a
the y-intercept.
Determine the coordinate of A.
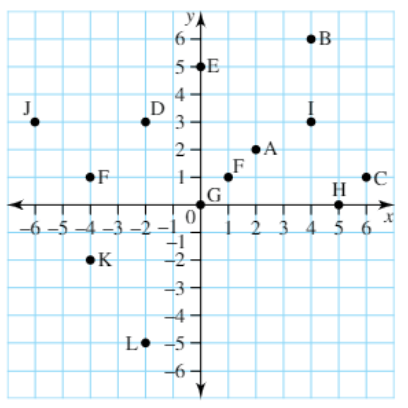
(2, 2)
Describe what a linear relationship is and provide 2 examples of a real-world scenario that uses linear relationships.
Things that change at a constant rate over time produce a straight-line graph and are known as a linear relationship. A car travelling at a constant speed, the interest earned by a simple-interest bank account, and a wage based on hours worked are all linear relationships.
Find b.
4b = 16
b = 4
State whether this line has a positive, negative, zero, or undefined gradient.
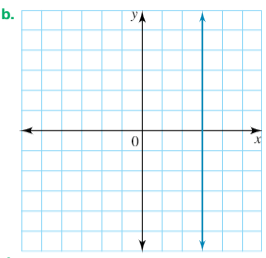
Undefined
Determine the y-intercept from the following rule.
y = 2x + 4
y-intercept = 4
Determine the coordinate of L.
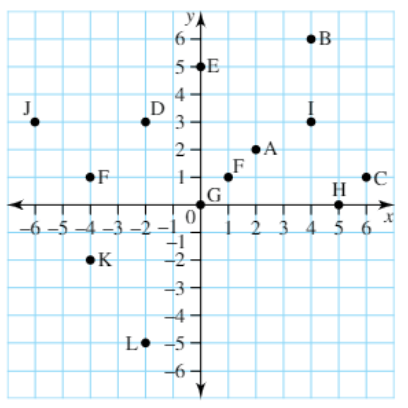
(-2, -5)
The graph shows the distance in km covered by two friends in a given time (hrs). How long had Friend A been travelling for, when she had travelled 25km?
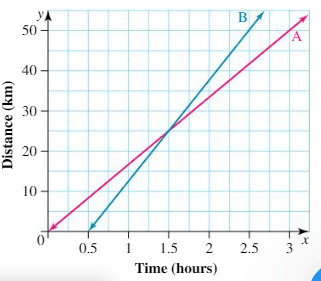
1.5 hours
Find a.
3a + 10 = 46
a = 12
Determine the gradient from this rule.
y = -2x + 3
gradient = -2
Determine the y-intercept from the following rule.
y = 5x - 3
y-intercept = -3.
Which quadrant will the following point be in:
(1, -2)
Quadrant 4 (iv)
Find y.
(y + 2) / 3 = 16
y = 46
Calculate the gradient from the following graph. Use m = (rise)/(run
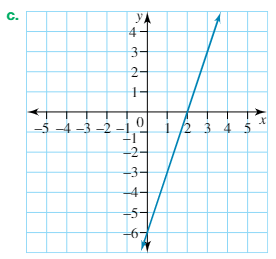
m = (rise)/(run)
m = 3/1
m = 3
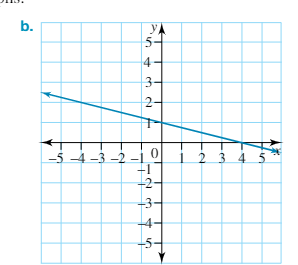
Determine the y-intercept from this graph.
y-intercept = 0
The following data is linear.
Using y = a + bx, what is the equation?

y = 3 + x
Kyle was very bored on his holidays and decided to measure how much the grass grew in his backyard.
The grass started at 10mm tall, and increased by 2mm each day.
Determine the linear rule that would represent this scenario.
y-intercept is the starting value = 10
gradient is the amount increasing or decreasing which is = 2.
Therefore the rule is y = 2x +10.
Find b.
b^2/20 = 5
b = 10
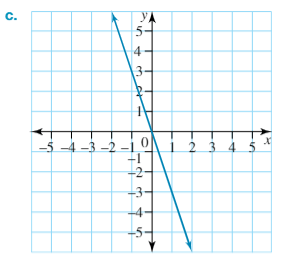
Determine the gradient of the following graph. Use m =
(rise)/(run)
m = (rise)/(run)
m = 1/4
m = 0.25
Determine the y-intercept from this graph.
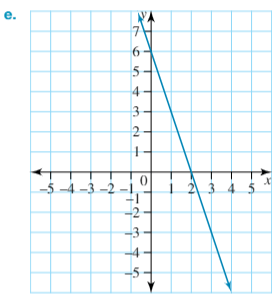
y-intercept = 6
Use the rule y = 2x + 1 to fill out the table of values.

-3, -1, 1, 3, 5
Chris's fridge is not working. He called a repair company and they are sending someone to repair the fridge. The company charges a $55 call out fee, plus $45 for each hour they are there.
Determine the linear rule to represent this scenario.
Then use that linear rule to calculate how much it will cost if the repair is there for 4 hours.
y-intercept is where it starts = 55
gradient is how much it is increasing or decreasing = 45
therefore y = 45x + 55
Substitute 4 into the x.
y = $235